皆さんこんにちは、はてなクマです。
今回は高校レベルの数学と物理を使って「ブラックホールに物体を落っことしたら、どんな運動をするのか?」ということを調べてみたいと思います。
物体をブラックホールの近くに置くと、徐々に重力によってブラックホールの方に引き寄せられ、だんだん加速して行きます。まるで、坂道の上に置いたボールがコロコロと転がり、だんだん速くなっていくように。
でも、坂道でボールを転がしたり地球上での物体の自由落下と異なるのは、重力そのものがどんどん強くなることです。高校の物理で出てくる自由落下問題は、物体に働く重力が一定と仮定しています。
ブラックホールに物体を落とす問題の場合は重力が位置の関数になるので、解くべき方程式が少し複雑になります。この記事では本格的な数式を使いますので、数式展開が必要のない方は「まとめ」まで読み飛ばしてくださいね。
それでは始めましょう。
問題を方程式に焼き直す
まずは問題をモデル化します。本来は時空の曲がりを記述できるアインシュタインの一般相対性理論を使う必要があるのですが、大変複雑な式を解くことになってしまいます。ですので、ここではニュートン力学の万有引力を使います。
話を間単にするために1次元のみに限定し、ブラックホールも、落っことす物体も質点とみなせるとしましょう。また、ブラックホールの質量の方が圧倒的に大きいため、実際に重力を感じて運動するのは物体の方で、ブラックホールは完全に静止しているとします。
このようなモデル化をすると、大気のない宇宙空間で質量\(m\)の物体に質量\(M\)のブラックホールから働く万有引力\(F\)次のように表されます。
$$F = \ – G\frac{mM}{r^2}$$\(G\)は万有引力定数です。図で表すとちょうどこんな感じでしょうか。
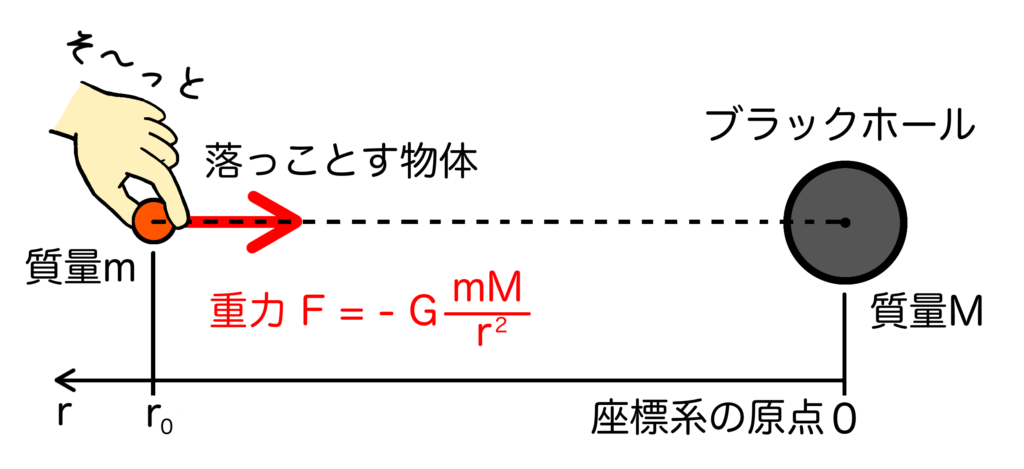
結構シンプルですよね。ただし、座標系の取り方に注意が必要です。問題を解きやすくするために座標の原点はブラックホールの位置にとります。物体を置くのはブラックホールから距離\(r_0\)だけ離れた地点とします。従って、重力は座標軸のマイナス方向に働くため、負の値になるのです。
実は重力を位置の関数で表せた時点で、ニュートンの運動方程式を用いて問題を解くことができます。ニュートンの運動方程式は「運動する物体の質量と加速度の積がその物体に働く力に等しい」というものです。加速度は位置の時間による2階微分なので、次のような式で表すことができます。
$$ m \frac{d^2r}{dt^2} = \ – G \frac{mM}{r^2}$$この微分方程式は一見シンプルですが、簡単には解けません。非線形の微分方程式は怖いですね〜汗
ですので、今回は「エネルギー保存則」から新しい式をつくります。この場合登場するのは運動エネルギーと重力によるポテンシャルエネルギーのみなので、力学的エネルギーの保存則とも言えます。
質量\(m\)の物体が速度\(v\)で動いている時の運動エネルギーは\(\frac{1}{2}mv^2\)です。一方、重力によるポテンシャルエネルギーは重力の式から求めることができます。
重力は保存力なので、単純に重力を距離で積分することによってポテンシャルエネルギー\(U\)を求めることができます。位置\(r\)にある物体のポテンシャルエネルギーは次のようになります。
$$U = \ -\int F dr = \ – G\frac{mM}{r}+C$$ここで出てきた積分定数\(C\)はポテンシャルエネルギーの基準を決めることによって定まります。通常は計算を簡単にするために重力源から無限遠の場所を基準にします。つまり、重力の影響を受けない\(\ r = \ \infty \)の無限遠において\(\ U = \ 0\)なので、\(\ C = 0\)となります。
従って「運動エネルギーと重力ポテンシャルエネルギーの総量が常に一定に保たれる」というエネルギー保存則を式で表現すると次のようになります。
$$\frac{1}{2}mv^2-G\frac{mM}{r}=E_0\mathrm{(一定)}$$\(E_0\)は初期状態におけるエネルギーを表しています。今考えている初期状態では、\(\ t = 0\)においてブラックホールから距離\(r_0\)の所に、物体をそ〜っと置きます。ですので初速度\(\ v_0 = 0\)ですね。よって、\(E_0\)は\(r_0\)におけるポテンシャルエネルギーのみになります。
$$E_0=-G\frac{mM}{r_0}$$以上より、解くべき方程式は次のようになります。
$$\frac{1}{2}mv^2-G\frac{mM}{r}=-G\frac{mM}{r_0}$$この式を\(v\)について解くと、
$$v= \ -\sqrt{2GM \left( \frac{1}{r}-\frac{1}{r_0} \right) }$$となります。ここで注意したいのは、平方根を外す時にマイナスをつけることです。今の座標系の設定だと\(v\)は常に負の値をとるので、マイナスをつけるのです。物体の速度\(v\)は位置\(r\)の時間\(t\)による1階微分ですから、次のような微分方程式が得られます。
$$ \frac{dr}{dt}= \ -\sqrt{2GM \left( \frac{1}{r}-\frac{1}{r_0} \right) }$$さて、これでようやく解くべき方程式が整いました。この微分方程式を解くことができれば、ブラックホールに落っこちていく物体の運動を知ることができます。
微分方程式を解く
与えられた微分方程式は1階非線型微分方程式です。先にネタばらしをしておくと、この微分方程式を解いても位置\(r\)を時間\(t\)の関数として表すことはできません。媒介変数表示によって間接的に\(r\)と\(t\)を関連づける形の関数になります。それでは解いて行きましょう。
まずは変数分離系なので\(r\)の関数部分を左辺に、\(t\)の関数を右辺に分離しましょう。
$$ -\left( \frac{1}{r} – \frac{1}{r_0} \right)^{-\frac{1}{2}} dr = \sqrt{2GM} dt$$右辺は簡単に積分できます。
$$ \mathrm{(右辺)} = \sqrt{2GM}t + C$$左辺は \(x = \frac{1}{r}\)と置くと、
$$\frac{dx}{dr} = -\frac{1}{r^2} = -x^2$$なので、
$$ \mathrm{(左辺)} = \ \int{ \left( x \ – \frac{1}{r_0} \right)^{-\frac{1}{2}} \left( \frac{1}{x^2} \right) dx } $$となります。さらに \(y = \sqrt{x – \frac{1}{r_0}}\)と置換すると、
$$ \frac{dy}{dx} = \frac{1}{2} \left( x \ – \frac{1}{r_0} \right)^{- \frac{1}{2}} $$なので、
$$ \mathrm{(左辺)} = 2 \int{ \left( y^2 \ – \frac{1}{r_0} \right)^{-2} dy} $$さらにさらに置換を使って行きます。今度は\( y = \sqrt{\frac{1}{r_0}} \tan \alpha \)とおくと、\(\frac{dy}{d\alpha} = \sqrt{\frac{1}{r_0}} \left( 1 + \tan^2 \alpha \right) \)なので、
$$ \begin{eqnarray} \mathrm{(左辺)} &=& 2 \int{ \frac{\sqrt{\frac{1}{r_0}} \left( 1 + \tan^2 \alpha \right)}{\left( \frac{1}{r_0} \tan^2 \alpha + \frac{1}{r_0} \right)^2 } d\alpha} \\ &=& 2 r_0^{3/2} \int{ \frac{\left( 1 + \tan^2 \alpha \right)}{\left( \tan^2 \alpha + 1 \right)^2 } d\alpha} \\ &=& 2 r_0^{3/2} \int{ \cos^2 \alpha } d\alpha \\ &=& 2 r_0^{3/2} \left( \alpha + \frac{1}{2} \sin 2\alpha \right) + C \end{eqnarray} $$最後に右辺と左辺をつなげて、積分定数をまとめれば解の完成で〜す!
$$ 2 r_0^{3/2} \left( \alpha + \frac{1}{2} \sin 2\alpha \right) = \sqrt{2GM}t + C $$さらに、\(\theta = \pi \ – 2 \alpha\)とおくと\(\alpha = \frac{\pi}{2} \ – \frac{\theta}{2}\)なので、
$$ \begin{eqnarray} \sqrt{2GM} t + C &=& r_0^{3/2} \left( \frac{\pi}{2}-\frac{\theta}{2} + \frac{1}{2} \sin \left( \pi \ – \theta \right) \right) \\ &=& \frac{1}{2} r_0^{3/2} \left( \pi \ – \theta + \sin \theta \right) \end{eqnarray} $$定数項を積分定数としてまとめなおすと、
$$ \sqrt{2GM} t + C = \ -\frac{1}{2} r_0^{3/2} \left( \theta \ – \sin \theta \right) $$さらに両辺を\(\sqrt{2GM}\)で割って、積分定数をまとめなおすと、
$$ t = \ C \ – \sqrt{\frac{r_0^3}{8GM}} \left( \theta \ – \sin \theta \right) $$一方で置換の過程から\(r\)の式を求めると、
$$ \begin{eqnarray} r &=& \frac{1}{x} \\ &=& \frac{1}{y^2+\frac{1}{r_0}}\\ &=& \frac{r_0}{\tan^2 \alpha + 1}\\ &=& \frac{r_0}{\tan^2 \left( \frac{\pi}{2} – \frac{\theta}{2} \right) + 1} \\ &=& \frac{1}{2} r_0 \left( 1 – \cos \theta \right) \end{eqnarray} $$となって、\(r\)も\(t\)も\(\theta\)の関数としてとてもきれいな形にまとまりました。
ここまで変数の置換を何回も行ってきました。ですので、最終的な変数として残っている\(\theta\)が一体何者なのか全然わかりません。ひとまず、最初の変数\(r\)から出発して、置換してきた各々の変数の変域を調べてみます。
$$ \begin{eqnarray} r&:& \quad r_0 \longrightarrow 0 \\ x&:& \quad 1/r_0 \longrightarrow \infty \\ y&:& \quad 0 \longrightarrow \infty \\ \alpha&:& \quad 0 \longrightarrow \pi/2 \\ \theta&:& \quad \pi \longrightarrow 0 \\ \end{eqnarray} $$従って、\(t = 0\)のとき\(\theta = \pi\)なので、ここから積分定数を求めると、
$$ \begin{eqnarray} 0 &=& C – \ \sqrt{\frac{r_0^3}{8GM}} \left( \pi – 0 \right) \\ C &=& \pi \sqrt{\frac{r_0^3}{8GM}} \end{eqnarray} $$以上より\(t\)は次のような\(\theta\)の関数として表すことができる。
$$ \left\{ \begin{array}{l} t(\theta) = \sqrt{\strut{\frac{r_0^3}{8GM}}} \lbrace \pi – \left( \theta – \sin \theta \right) \rbrace \\ r(\theta) = \frac{1}{2} r_0 \left( 1 – \cos \theta \right) \end{array} \right. $$もう皆さんはお気づきだと思いますが、導いた距離と時間の式には落っことす物体の質量\(m\)が全く入っていません。つまり、どんな重さの物体を落とすかは全く関係なく、全ての物体が同じ運動方程式に従ってブラックホールに落っこちることがわかります。
ブラックホールに落っこちる物体の方程式を図示してみる
ここまでの計算によって明らかになった、ブラックホールに落っこちる物体が従う方程式は、一体何を表しているんでしょうか?
実は\(\theta\)によって関連づけられた\(r\)と\(t\)の方程式は、サイクロイドという関数の仲間です。サイクロイドは高校数学で出てくる媒介変数表示の関数で、次のようなものです。
$$ \left\{ \begin{array}{l} x(\theta) = \left( \theta – \sin \theta \right) \\ y(\theta) = 1 – \cos \theta \end{array} \right. $$すごく似てますよね!このサイクロイドは半径1の円を\(x\)軸上を転がした時に、特定の1点が描く軌跡が作る関数なのです。
ブラックホールに落っこちる物体も、このサイクロイドに従ってブラックホールに落ち込んでいくことになります。では、実際にこの関数を図示してみると次のようになります。
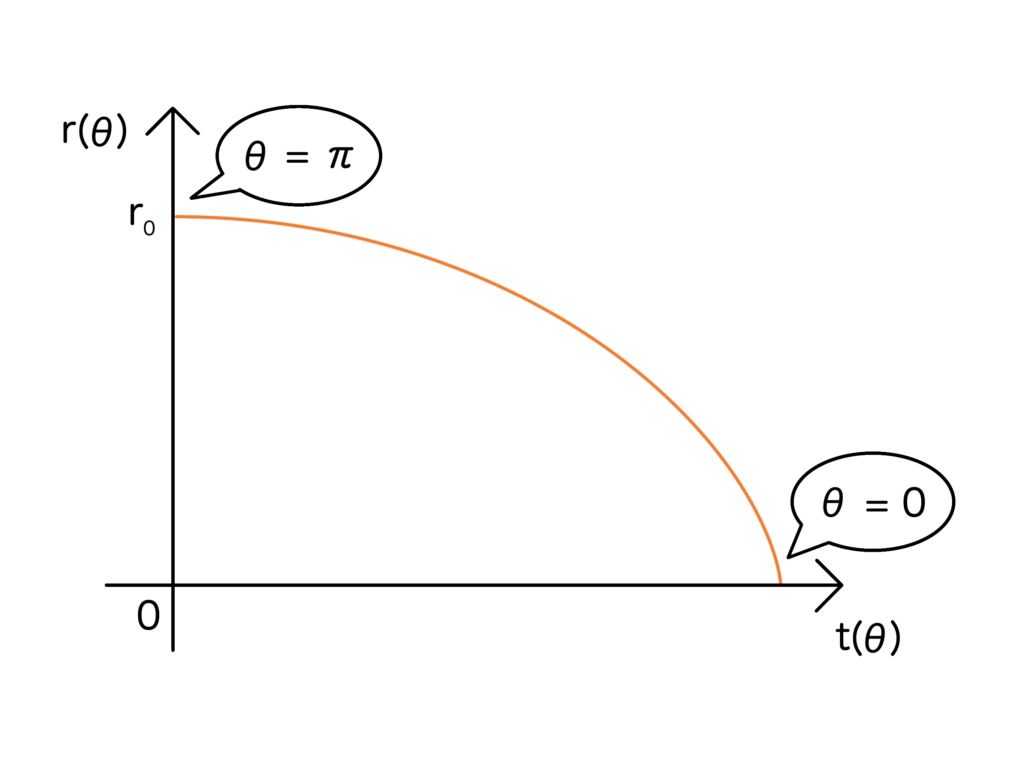
時刻\(t = 0\)の時は初速度0で、ゆっくり転がり始めます。ブラックホールに近づくにつれ、重力がどんどん大きくなり、距離の縮まり方も早くなります。
光さえも出てこられないシュヴァルツシルト半径を求める
ブラックホールに向かって落っことした物体は、そのあと一体どうなってしまうのでしょうか?
最終的に物体がブラックホールの中心点に到達した時、現代科学ではその物体の様子を知るすべはありません。
さらに、ブラックホールに落っこちる物体はブラックホールの中心点に到達する前に、ある特殊な境界面を通過します。それが光さえも脱出することのできないシュヴァルツシルト半径と呼ばれる領域です。
実際にブラックホールに向かっている物体からは、シュバルツシルト半径は周りの宇宙空間と変わらず、なにか特殊な膜などが存在するわけではありません。
しかし、ブラックホールの遠くから観察している人から見るとシュバルツシルト半径を越えた物体から出る一切の情報は、ブラックホールの外側には出てこなくなってしまうため、文字通り「穴に落っこちた」状態になります。
シュバルツシルト半径という境界の向こう側で何が起きているのかは知ることができません。ですので、ブラックホールの周りにあるシュヴァルツシルト半径の球面のことを『事象の地平面(event horizon)』と呼びます。
では実際にシュヴァルツシルト半径を求めてみましょう。実は、一般相対性理論によって予言されるブラックホールを特徴付けるシュバルツシルト半径ですが、ニュートン力学からも全く同じ数式を求めることができます。
エネルギー保存則から出発します。シュバルツシルト半径の意味をエネルギーで考えてみると、物体がたとえ光速で運動していたとしても重力ポテンシャルによってブラックホールに引きずり込まれてしまう距離です。つまり、光速で運動する物体の運動エネルギーと重力によるポテンシャルエネルギーがちょうど釣り合う距離、ということになります。
正確には物体は光速を超えることはできませんし、光速に近い物体の運動を記述するためには相対性理論を使う必要がありますが、このようなモデル化によってシュバルツシルト半径を導出することができます。
エネルギー保存則の式は次のようになります。
$$\frac{1}{2}mc^2-G\frac{mM}{r}=0$$ここで、\(c\)は光速を表しています。この式を\(r\)について解くと、
$$r=\frac{2GM}{c^2}$$となりシュヴァルツシルト半径が求まります。
太陽がブラックホールになったらどのくらいの時間で吸い込まれてしまうのか?
それではここまで導出してきた式を使って実際に物体の運動を計算してみましょう。面白いモデルケースとして、もし太陽がブラックホールになってしまった場合のことを考えてみましょう。
恒星進化論からすると、太陽程度の質量を持つ恒星がブラックホールになることはあり得ません。しかし、もしなんらかの力が働いて太陽が無限に圧縮され続けていけばいつかはブラックホールになるはずです。
まずは、太陽がブラックホールになるためにはどれくらいの半径まで圧縮される必要があるかを考えてみます。
ブラックホールになるためには天体の直径はシュヴァルツシルト半径以下でなくてはなりません。実際に太陽の質量(\(M = 2.0 \times 10^{30} \mathrm{kg}\))と光速(\(c = 3.0 \times 10^{8} \mathrm{m/s}\))、そして万有引力定数(\(G = 6.7 \times 10^{-11} \mathrm{m^3 /kg \ s^2}\))をシュヴァルツシルト半径の数式に代入してみると次のようになります。
$$ \begin{eqnarray} r &=& \frac{2 \times (6.7\times 10^{-11}) \times (2.0 \times 10^{30}) }{(3.0 \times 10^8)^2} \\ &\approx& 3.0 \times 10^3 \end{eqnarray} $$つまり、太陽をブラックホールにするには半径\(3 \mathrm{km}\)以下にすればいいことになります。
それでは、太陽が突然ブラックホールになってしまった時、地球上から太陽に向かって落ちていく物体はどれくらいの時間でブラックホールに吸い込まれてしまうのでしょうか?
実際は地球は太陽の周りを公転しているので、すぐにブラックホールに吸い込まれることはありませんが、もし地球から太陽に向かってまっすぐ落ちていったとすると、どのような運動をするのかを計算してみましょう。
地球と太陽の距離は1億5000万キロメートルです。このスケールからするとブラックホールになった太陽の半径3kmなんて誤差の範囲ですよね。つまり地球上(\(r_0 = 1.5 \times 10^8 \mathrm{km}\))から放たれた物体が太陽(\(r = 0 \ \mathrm{km}\))まで到達する時間を求めればいいことになります。
先ほど求めた運動方程式をもう一度思い出してみましょう。
$$ \left\{ \begin{array}{l} t(\theta) = \sqrt{\strut{\frac{r_0^3}{8GM}}} \lbrace \pi – \left( \theta – \sin \theta \right) \rbrace \\ r(\theta) = \frac{1}{2} r_0 \left( 1 – \cos \theta \right) \end{array} \right. $$この式で\(\ r = 0\)を代入すると\(\ \theta = 0\)となるので、これを\(t\)の式に代入します。
$$ t = \pi \sqrt{\frac{r_0^3}{8GM}} $$さらに具体的な値を入れて計算をしてみましょう。
$$ \begin{eqnarray} t &=& \pi \sqrt{\frac{(1.5 \times 10^{11})^3}{8 \times (6.7 \times 10^{-11}) \times (2.0 \times 10^{30})}} \\ &\approx& 5.6 \times 10^6 \end{eqnarray} $$つまり地球上にある物体は560万秒でブラックホールに飲み込まれてしまうことになります。時間に直すと大体1600時間、日に直すと大体65日です。
まとめ
太陽がブラックホールになってしまった時、地球上にそっと置いた物体はサイクロイド曲線で表される時間と位置の関係に従い、およそ2ヶ月でブラックホールまで落っこちてしまいます。
ここで得られた方程式は太陽がブラックホールにならなくても成り立ちます。ただし、太陽の表面に到着した時の物体の速度は秒速617キロメートル、そして太陽の半径は70万キロメートルなので、太陽表面から中心まで太陽の表面までは20分もかかりません。
ブラックホールに落ち込む物体の運動方程式はエネルギー保存則を用いることによって導出することができます。また、物体の位置と時刻の関係はサイクロイド曲線によって表されることがわかりました。得られた運動方程式に具体的な値を代入することで様々な状況を計算できるので、是非みなさんも試してみてください。