【徹底比較】〜元金均等と元利均等はどちらが得か？〜

皆さんこんにちは、はてなクマです。

ローンの返済方式には大きく分けて元利均等と元金均等があります。

一般的には、元利均等は毎月定額の返済だからわかりやすいけど利息が高くつく、元金均等は利息は安く済むけど初期の返済額が大きくなるとイメージしている方が多いと思います。

それではどちらの返済方式がどのくらいお得なのか、ということを具体的に計算することはできますか？

一見複雑な計算が必要なように思えますが、実は高校レベルの数学を使うことで返済金額や利息の計算式を導くことができます。

今回は『元利均等方式と元金均等方式のローン返済の方程式を比較し、どちらがどのくらいお得なのか』を検証してみたいと思います。

元利均等方式と元金均等方式の違い

具体的な計算をする前に、まずはそれぞれの返済方式の特徴とメリット・デメリットについてまとめておきます。

元利均等方式のメリット・デメリット

元利均等方式は元金と利息を合わせた返済金額が返済期間中ずっと定額で支払っていく返済方式です。

毎月の返済金額が定額であるため日々の生活において支出計画を立てやすい点がメリットと言えるでしょう。

一方、返済初期は返済金額に占める利息分が大きく、なかなか元金が減っていきません。そのため、元金均等方式と比べて利息総額が高くなるというデメリットがあります。

元金均等方式のメリット・デメリット

元金均等方式は毎月定額の元金を返済していく返済方法です。元金部分は定額返済ですが、それに伴って発生する利息は毎月変動していくので、月々の支払額も変化します。

メリットとしては毎月定額の元金返済を行うので元金の減少速度が早く、利息総額を抑えられる点が挙げられます。

一方、返済初期は定額の元金返済に加え大きな利息が上乗せされるため、ひと月あたりの返済金額が高額になり家計を圧迫するというデメリットもあります。

返済方式のイメージ

それぞれの返済方式による支払いの具体的なイメージを掴むために、モデルケースとして500万円を年利10％、返済期間5年で借りた場合についてのグラフを作りました。

金利の安い現在では年利10％という高金利はカードローンやリボ払いでしか起こり得ませんが、利息が大きくなるので元利均等と元金均等の特徴は分かりやすくなります。

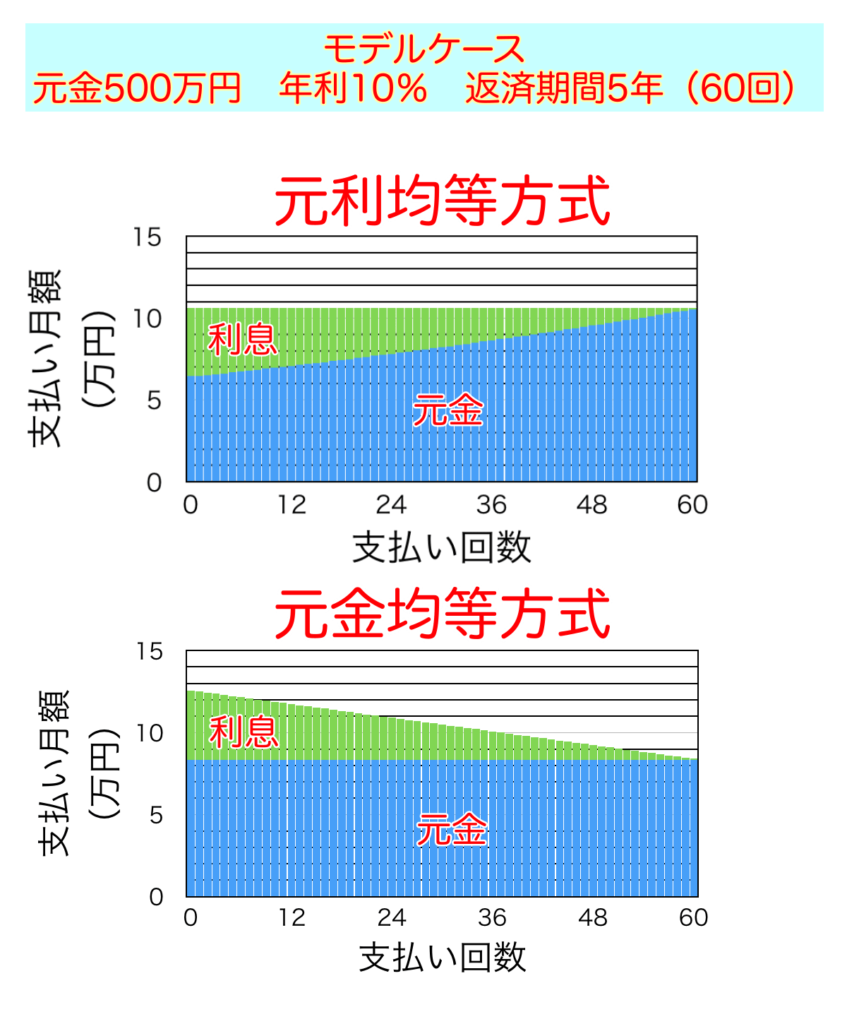
元利均等と元金均等の特徴が一目瞭然ですね。このモデルケースの場合、元利金等は返済期間を通じて10万6235円を支払うことになりますが、元金均等では12万5000円から8万4027円まで支払額が変化しています。

利息総額の計算式

借金の返済金額は借入総額\(M_0\)、金利（月利）\(p’\)、返済回数\(n\)の３つの数字から計算することができます。高校数学に出てくる級数という概念を使うことで、簡単に計算できる方程式を導くことができます。

ここで用いる金利\(p’\)とはよく使われている1年間の金利（年利）ではなく、1ヶ月あたりの金利、すなわち月利です。月々の返済額や利息を計算する上では月利の方が便利です。

年利を12で割れば月利をを求めることができます。
詳しい解説はこちらをご参照ください。
ローンの毎月の利息はどうやって決まるの？　簡単に計算する方法を解説

元利均等と元金均等の場合、支払う利息の総額も異なります。詳しい方程式の導出は別の記事で解説してます。
【借金の方程式を導く！】元利均等編
【借金の方程式を導く！】元金均等編

ここでは結果の方程式だけを確認します。借入総額\(M_0\)、金利（月利）\(p’\)、返済回数\(n\)のときの利息総額は次の方程式で計算できます。

具体的なケースで利息総額を計算してみる

300万円を年利3％、返済期間5年で借りる場合

自動車をローンで購入する場合を想定して借入総額300万円、年利3%、返済期間5年という設定で計算してみましょう。

方程式に代入するために少し準備をします。まず年利3%を12で割って月利に直します。

さらに%（パーセント）表示を100で割って割合表示に直します。

また、返済期間5年は60ヶ月なので返済回数は60回です。以上より借入総額\(M_0 = 300万円\)、金利（月利）\(p’ = 0.0025\)、返済回数\(n = 60\)として計算します。

これらの値をもとに利息総額は次のように計算できます。

• 元利均等：23万4364円
• 元金均等：22万8750円

元利均等と元金均等で利息の差額は 5,614円 でした。5年間の利息でこれくらいの差であればほとんど変わらならいと思っていいのではないでしょうか。

3000万円を年利1%、返済期間30年で借りる場合

今度は住宅を購入する場合を想定して、借入総額3000万円、年利3%、返済期間5年という設定で計算してみましょう。

先ほどと同様に年利1%は割合表示の月利に直すと 0.000833… になります。返済期間30年は360ヶ月なので、返済回数も360回です。

これらの値をもとに利息総額は次のように計算できます。

• 元利均等：473万7068円
• 元金均等：451万2500円

さすがに借入額や返済回数が大きくなると、支払う利息も高額になりますね。返済期間の30年で割ると約15万円の利息を毎年支払っていることになります。毎月に直すと約1万3千円ですね。

ただし、元利均等と元金均等の差は 22万4568円 でした。安くはない額ですが返済期間が30年だと毎年の差は 7,486円 なので、そこまで大きい額ではないのでしょうか。

この計算から、『元利均等方式による返済は毎年約7,500円の手数料（利息）を余分に支払うことで、1ヶ月あたりの返済が定額になり、初期返済時のゆとりや家計設計のしやすさを享受することができるサービス』と考えることもできます。

もし、この余分な利息を支払っても家計管理のメリットが重要だと思う場合は元利均等を選択すればOKですね。

返済方式が重要になるケース

ここまで見て来たように、返済方式の違いによる利息の差額は借入総額と比較するととても小さい額でした。現在の金利では返済方式の違いによる利息総額への影響は極めて小さいと言えるでしょう。

それではどのような場合に元利均等と元金均等の差が大きくなるのでしょうか？

すでにお分かりかもしれませんが、ズバリ金利が高い時です。バブル真っ最中の1991年当時は住宅ローンの金利が8%にもなっていました。

バブル期真っ最中にマイホームを購入したとして、借入総額3000万円、年利8%、返済期間30年という設定で利息総額を計算してみましょう。

• 元利均等：4924万6573円
• 元金均等：3610万円

これは返済総額ではありませんよ。利息分だけでこの金額になります。いやいやいや、マイホーム2件買えるやん！という結果になってしまいました。

バブル期は金融資産の利回りも良かったですが、逆に借金をする場合はものすごい利息を支払う必要があったんですね。今では頭金0で家や車を買うこともよくありますが、バブルの時は頭金なしで家を買うなんて正気の沙汰ではありませんでした。

話を元に戻して元利均等と元金均等の差額を見てみると 1314万6573円 です。差額だけでこの額になってしまいます。1年あたりに直しても43万円です。つまり、高い金利の場合は元金均等方式による返済で、元金をいち早く返すことによって利息がかなり減額されると言うことです。

月々の返済額が大きくなったとしても、年間で40万円もの利息節約になるのであれば、元金均等方式を選択するメリットはとても大きいですよね。

まとめ

いかがでしたか？

この記事では元利均等方式と元金均等方式での利息総額を計算するための方程式を紹介し、いくつかのケースで利息の差額がどれくらいになるのかを計算してみました。

結論として『現在の低い金利ではどちらの返済方式を選んだとしても利息は大きく変わらないが、バブル期のような高い金利でローンを組む場合は元金均等方式を選択することによって利息がかなり減額できる』ということがわかりました。

これからローンを組もうとしている方、もしくはすでに返済を始めている方も一度ご紹介した方程式を使って利息がどのくらいになるのか調べてみると家計管理に役立つかもしれません。