【借金の方程式を導く！】元金均等編

マネー

皆さんこんにちは、はてなクマです。

ローンの返済方法のうち、毎月定額の元金を返済していくやり方を元金均等方式と言います。元金均等方式での返済は、毎月定額の元金を返済するため、利息の総支払額が少なくなりますが、初期の返済額が高額になる、という側面もあります。皆さんは元金均等でローンの返済を行う時、月々の支払額や利息などはどのくらいになるかイメージできますか？

普通、ローンを組むときは車のディーラーやハウスメーカーの営業マンに説明を受けますが、彼らの言うこと全てを鵜呑みにしてしまうと、想像以上に多くの利息を支払うことになってしまうかもしれません。

自分で納得したローンを組むためにも、まずは借入総額に対して月々の支払いや利息がどのくらいの金額になるのかをしっかり把握しないといけないですよね。

そこで今回は前回に続き、『元金均等方式で論を組んだ時の利息を計算するための方程式』を高校レベルの数学を使って導きます。

目次

借金の方程式（元金均等）を導く

必要な数の定義

まず、方程式を作るために必要な数字を次のように定義します。

  • 元金：\(M_i\)
  • 支払い回数：\(n\)
  • 金利（年利）：\(p\)
  • 月々の支払額：\(x_i\)

ここでは話を簡単にするためにボーナスによる支払いは考えないことにします。

支払額\(x_i\)と元金\(M_i\)の下に付いている\(_i\)は\(i\)回目の支払い額と、支払った後に残っている元金を意味します。つまり支払いを0回した時の元金\(M_0\)は借入総額を意味しますし、\(n\)回目の最後まで支払いを完了した時の元金\(M_n\)は0ということになります。

また、元金均等方式では月々の支払額が毎月変動していきます。つまり、支払月を\(i\)とすると、\(x\)は\(i\)の関数になるわけですね。

さて、次に金利についてもう少し考えます。

普通、ローンの借入先から提示されるのは『年〇〇％』という1年当たりの金利（年利）です。しかし、返済は月単位で行うことになるので、1カ月当たりの金利（月利）に直しておいた方が便利そうです。

これはそんなに難しくなくて、1年は12カ月なので年利を12で割れば月利を求めることができます。最初に定義した金利（年利）\(p\) を12で割って次のように月利を定義しなおしておきます。

$$(月利) \ p’ = (年利) \ p \div 12$$

これで準備が整いました。いよいよ実際に方程式を組み立てていきます。まず初めにやることは\(M_i\)、\(n\)、\(p’\)を使って\(x_i\)を表すことです。\(x_i\)を数式で表すことができれば、そこから利息や支払い総額を計算することができます。

\(i\)回目の支払い後元金についての方程式をつくる

元金均等方式の特徴は毎月定額の元金返済を行うことです。毎月返済する元金は借入総額\(M_0\)を返済回数\(n\)で割れば求まります。

$$\begin{eqnarray} （毎月返済する元金）=\frac{M_0}{n} \end{eqnarray}$$

つまり\(i\)回目の支払い後に残っている元金\(M_i\)は次の式で表せます。

$$\begin{eqnarray} M_i = M_0 – \frac{i M_0}{n} \end{eqnarray}$$

月々の支払額についての方程式をつくる

まず、『1回目の返済額\(x_1\)』を数式で表してみましょう。

元金均等方式の場合、借入総額\(M_0\)を返済回数\(n\)で割った毎月定額の元金を返済していきます。一方で、利息は元金によって変化していきます。1回目の返済時に支払う利息は借入総額\(M_0\)に月利\(p’\)をかけた額になります。つまり1回目の返済金額は次の式で表されます。

$$x_1 = \frac{M_0}{n} + M_0 p’$$

前述の通り右辺第1項が元金を、第2項が利息を表しています。それでは2回目はどう表されるでしょうか。元金の部分は1回目と同じですが、利息の部分が1回目の支払い後に残っている元金\(M_1\)に月利\(p’\)をかけたものになります。

$$x_2 = \frac{M_0}{n} + M_1 p’$$

ここまでの定式化でお気づきのように、\(i\)回目の支払い額も同様に表すことができます。

$$\begin{eqnarray} x_i &=& \frac{M_0}{n} + M_{i-1} p’\\ &=& \frac{M_0}{n} + \bigg( M_0 – \frac{(i-1) M_0}{n} \bigg) p’ \tag{1} \end{eqnarray}$$

元金均等方式は元利均等方式と異なり月々の返済金額はとても簡単な式で表されます。次は返済期間全体での支払い総額を計算してみましょう。

返済総額を計算する

支払い総額を\(X\)とすると、元利均等方式による支払い総額は次の式で表されます。

$$\begin{eqnarray} X &=& \sum_{i=1}^{n} x_i \\ &=& \sum_{i=1}^{n} \bigg\{ \frac{M_0}{n} + \bigg( M_0 – \frac{(i-1) M_0}{n} \bigg) p’ \bigg\} \tag{2} \end{eqnarray}$$

\(i\)が含まれていない項の和は単純に\(n\)をかけるだけです。式(2)をもう少し整理してみます。

$$\begin{eqnarray} X &=& M_0 + n M_0 p’ – \frac{M_0 p’}{n} \sum_{i=1}^{n} (i-1) \\ &=& M_0 + n M_0 p’ + M_0 p’ – \frac{M_0 p’}{n} \sum_{i=1}^{n} i\tag{3} \end{eqnarray}$$

ここで登場した\(\sum_{i = 1}^{n} i\)は等差級数と呼ばれ、和の記号を外すための公式があります。等差級数の公式より、

$$\begin{eqnarray} \sum_{i=1}^{n} i = \frac{1}{2}n(n+1) \end{eqnarray}$$

なので、式(3)は次のようになります。

$$\begin{eqnarray} X &=& M_0 + (n+1) M_0 p’ – \frac{(n + 1) M_0 p’}{2}\\ &=& M_0 + \frac{1}{2}(n + 1) M_0 p’ \tag{4} \end{eqnarray}$$

ようやく、元金均等方式の方程式を導くことができました。式(4)をよくみると、右辺第1項が借入総額\(M_0\)になっています。ということは、右辺第2項が利息の総額ということになります。

それではこの式を使って元金均等方式での具体的な返済例を見てみましょう。

借金の方程式（元金均等）からわかること

支払い総額と利息総額

元金均等方式でローンを組んだ場合の支払い総額と利息総額をまとめると次のようになります。

  • 支払総額：　\(M_0 + \frac{1}{2}(n + 1) M_0 p’\)
  • 利息総額：　\(\frac{1}{2}(n + 1) M_0 p’\)

利息率

借金返済における利息の大きさを知る上で重要になるのが『利息率』です。毎月定額返済を行う元利均等方式ですが、返済金額に対する利息の割合は毎月変化していきます。

実際に支払っている金額のうち何％が利息、すなわち手数料なのかがわかると、お金を借りるということに対するリスクをしっかりイメージすることができます。

利息率は利息を返済額で割れば求まりますので、元金均等方式における利息率は式(1)からすぐに計算できます。任意の返済回（\(i\)回目）での利息率は、

$$\begin{eqnarray} （利息率）&=& \frac{\bigg\{ M_0 – \frac{(i-1) M_0}{n} \bigg\} p’}{\frac{M_0}{n} + \bigg\{ M_0 – \frac{(i-1) M_0}{n} \bigg\} p’} \\ \\ &=& \frac{( n – i + 1 ) p’}{1 + ( n – i + 1 ) p’} \\ \\ &=& \Big[ \big\{ (n – i + 1) p’ \big\}^{-1} +1 \Big]^{-1} \end{eqnarray}$$

と表すことができます。

具体例で計算してみる

次のような具体例を用いた月々の返済額を計算してみましょう。

  • 借入総額：500万円
  • 返済期間：5年
  • 年利：3%

方程式に入れるために、与えられた数値の単位を変換します。まず返済期間5年というのは月に変換すると60カ月になります。また、年利3％を割合表示の月利に変換すると月利0.0025になります。

まず、全返済期間における支払総額と利息総額を計算してみましょう。設定値\(M_0 = 500\)万円、\(p’=0.0025\)、\(n=60\)を支払総額と利息総額の式に代入して計算すると次のようになります。

  • 支払総額：5,381,125 円
  • 利息総額： 381,125 円

500万円を金利3%で5年間借りると約38万円の手数料がかかることがわかりました。毎月の支払い額の推移を表すグラフは次のようになります。

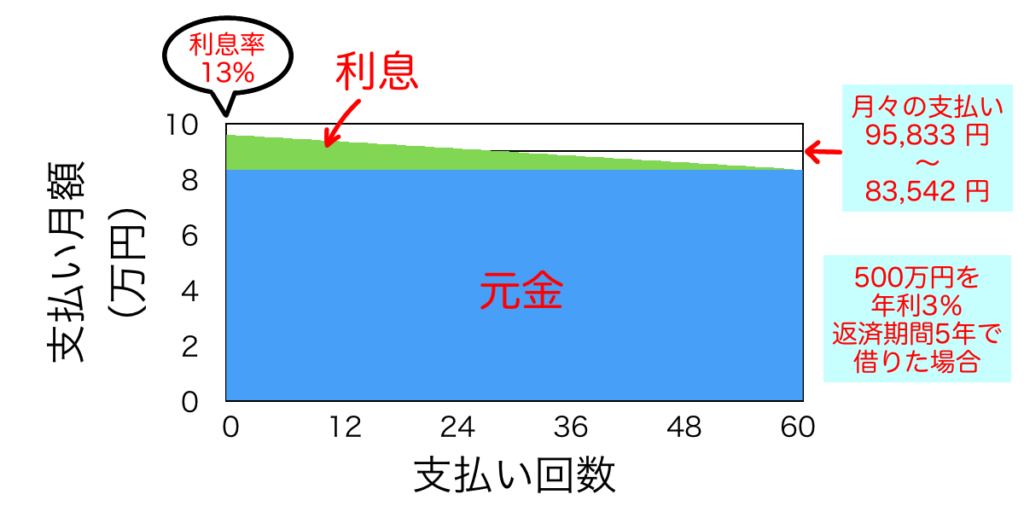
今回設定した条件では返済開始直後は利息率が約13％でした。元金均等方式では初めの返済額が95,833円と高額ですが、徐々に下がっていき、最終的には83,542円になることがわかります。

まとめ

いかがでしたでしょうか。

元金均等方式での支払い総額は高校数学で出てくる等差級数という考え方を使うことで方程式をつくることができました。

この方程式に借金の条件を代入して計算すれば、月々の返済額や利息率などが計算できます。これからローンを組むことを考えている方、もしくはローンの返済中の方は、一度この方程式を使って利息率を計算してみてはどうでしょうか？

最新情報をチェックしよう！

マネーの最新記事8件