【借金の方程式を導く！】元利均等編

マネー

皆さんこんにちは、はてなクマです。

ローンを組んだ時、返済額が毎月定額であり、わかりやすいため利用されることの多い『元利均等方式』。

皆さんはローンの借入額から月々の返済における利息はどれくらいか？　また期間全体で支払うことになる利息の総額はいくらか？　など計算できますか？

普通はローンを組むときは専門の人に説明を受けながら書類を作成しますが、彼らが強調するのは月々の返済額だけ…

しっかり自分の頭で考えないと知らないうちに多額の利息を支払っていた、なんてことにもなりかねません。

そこで今回は高校レベルの数学を使って『元利均等方式でローンを組んだ時の利息を表す方程式』を導いてみましょう。

目次

借金の方程式（元利均等）を導く

必要な数の定義

まず、方程式を作るために必要な数字を次のように定義します。

  • 元金：\(M_i\)
  • 支払い回数：\(n\)
  • 金利（年利）：\(p\)
  • 月々の支払額：\(x\)

意外にも複雑な借金の返済形式であっても、この4つの数字だけで方程式を作ることができます。ただし、ここでは話を簡単にするためにボーナスによる支払いは考えないことにします。

元金\(M_i\)の下に付いている\(_i\)は\(i\)回目の支払いの時に残っている元金を意味します。つまり支払いを0回した時の元金\(M_0\)は借入総額を意味しますし、\(n\)回目の最後まで支払いを完了した時の元金\(M_n\)は0ということになります。

さて、次に金利についてもう少し考えます。

普通、ローンの借入先から提示されるのは『年〇〇％』という1年当たりの金利（年利）です。しかし、返済は月単位で行うことになるので、1カ月当たりの金利（月利）に直しておいた方が便利そうです。

これはそんなに難しくなくて、1年は12カ月なので年利を12で割れば月利を求めることができます。最初に定義した金利（年利）\(p\) を12で割って次のように月利を定義しなおしておきます。

$$(月利) \ p’ = (年利) \ p \div 12$$

これで準備が整いました。いよいよ実際に方程式を組み立てていきます。先に少しだけ見通しについて触れておきます。

最初に定義した４つの数字のうち、元金\(M_i\)、支払い回数\(n\)、金利\(p\)は私たちが決めることのできる既知数です。一方で、月々の支払額\(x\)は現時点ではいくらなのかわかりません。そして元利均等方式による返済の場合、この\(x\)は定数になります。

そのため、まず初めにやることは\(M_i\)、\(n\)、\(p\)を使って\(x\)を表すことです。\(x\)を数式で表すことができれば、そこから利息を計算することができます。

支払い後に残る元金についての方程式をつくる

まず、『1回目の返済を行った後に残っている元金\(M_1\)』を数式で表してみましょう。

この残りの元金は借入総額\(M_0\)に利息を足して、さらに月々の返済額\(x\)を引けば求まります。1回目の返済時に発生する利息は借入総額\(M_0\)に月利\(p’\)をかければ求まります。言葉ので数式を表すと次のようになります。

$$ (1回目返済後の元金) = (借入総額) \ + \ (利息) \ – \ (1カ月の返済額) $$

数式で表すと次のようになります。

$$\begin{eqnarray} M_1 &=& M_0 + M_0 p’ \ – \ x \\ &=& (1 + p’)M_0 \ – \ x \tag{1} \end{eqnarray}$$

さて、それでは2回目の支払いはどうなるでしょうか。2回目の支払いを終えた後に残る元金\(M_2\)は、1回目返済後の元金\(M_1\)に利息を足し、さらにそこから月々の返済額を引けば求まります。つまり式で表すと次のようになります。

$$\begin{eqnarray} M_2 &=& M_1 \ + \ M_1 p’ \ – \ x \\ &=& (1 + p’)M_1 \ – \ x \tag{2} \end{eqnarray}$$

ここで式(1)を式(2)に代入して整理すると、

$$\begin{eqnarray} M_2 &=& (1 + p’) \{(1 + p’)M_0 \ – \ x \} \ – \ x \\ &=& (1 + p’)^2 M_0 \ – \ (1 + p’) x \ – \ x \\ \end{eqnarray}$$

なんとなく規則性が見えてきました。同様にして3回目、4回目の支払い以降も元金を計算してみましょう。

$$\begin{eqnarray} M_1 &=& (1 + p’)^1 M_0 \ &-& \ x \\ M_2 &=& (1 + p’)^2 M_0 \ &-& \ (1 + p’) x \ &-& \ x \\ M_3 &=& (1 + p’)^3 M_0 \ &-& \ (1 + p’)^2 x \ &-& \ (1 + p’) x \ &-& \ x \\ M_4 &=& (1 + p’)^4 M_0 \ &-& \ (1 + p’)^3 x \ &-& \ (1 + p’)^2 x \ &-& \ (1 + p’) x \ – \ x \\ \end{eqnarray}$$

どうやら右辺の第1項は\((1+p’)\)のべき乗の数字が1つずつ増えているだけですね。右辺の第2項から先は、べき乗の項そのものが1つずつ増えています。次にここから式の法則性を見つけて、一般化することを目指します。

数式から規則性を見つけて\(n\)回目の式に一般化する

それでは任意の支払い回数\(n\)回目について式を作ります。

$$\begin{eqnarray} M_n &=& (1 + p’)^n M_0 \ \ – \displaystyle \sum_{i=0}^{n-1} (1 + p’)^i x \tag{3}\\ \end{eqnarray}$$

この式で新たに登場した\(i\)は総和を取るためのカウントに用いる文字ですので特に重要な意味はありません。

式(3)で厄介なのは\(\sum\)のついた和に関する項です。まずはこの部分だけを考えましょう。\(x\)は全ての項に共通する因数ですので和の記号の外に括り出すことができます。

$$ \displaystyle x \sum_{i=0}^{n-1} (1 + p’)^i $$

和の部分に注目すると、『等比級数』であることに気づきます。この等比級数は高校レベルの数学に登場するもので、簡単な公式で計算することができます。公式の導出自体もそんなに難しくなので、少し考えてみると面白いかもしれません。

ここでは等比級数の公式だけをおさらいすることにします。初項\(a\)、公比\(r\)の等比級数の公式は次のようになります。

$$ \displaystyle \sum_{i=1}^{n} a r^{i-1} = a + a r + a r^2 + \cdots = \frac{a (1-r^n)}{1-r} \ \ \ (ただし、r \neq 1)$$

私たちの導いた方程式において、初項は\(1\)、公比は\((1+p’)\)なので、

$$ \displaystyle x \sum_{i=0}^{n-1} (1 + p’)^i = x \frac{1-(1+p’)^n}{1-(1+p’)} = \ – \frac{x}{p’}\{1-(1+p’)^n\}$$

これで\(\sum\)が外れて計算しやすい形になりました。この結果を式(3)に戻してやると、次のようになります。

$$\begin{eqnarray} M_n &=& (1 + p’)^n M_0 \ + \frac{x}{p’}\{1-(1+p’)^n\} \tag{4}\\ \end{eqnarray}$$

これで一般化された方程式が完成しました。次はいよいよ\(x\)を求めます。

月々の返済額\(x\)について式を解く

目的をもう一度おさらいすると、私たちは元利均等方式でローンを返済する時の、月々の返済金額を表す方程式を導きたいのでした。

\(n\)回目の支払い\(M_n\)に一般化した式(4)を見てみると、月利\(p’\)、借入総額\(M_0\)、支払い回数\(n\)、そして月々の返済金額\(x\)についての式になっています。この式を\(x\)について解くことができれば、月々の返済金額や利息がどれくらいになるのかを計算することができます。

\(n\)回目でローンは全て返し終わるはずなので、\(n\)回目の支払いが終わった後の元金\(M_n\)は\(0\)ですから、

$$\begin{eqnarray} 0 &=& (1 + p’)^n M_0 \ + \ \frac{x}{p’}\{1-(1+p’)^n\}\\ \end{eqnarray}$$

となります。この式を\(x\)について解くと次のようになります。

$$ x = \frac{M_0 p’}{1-(1+p’)^{-n}} \tag{5}\\ $$

これで元利均等方式による方程式の解が得られました。この方程式を使ってどんなことがわかるか見ていきましょう。

借金の方程式（元利均等）からわかること

支払い総額と利息総額

元利均等方式による借金の場合、月々の返済額\(x\)さえ求めてしまえば、全返済期間での支払総額や利息総額は次のように簡単に計算できます。

  • 支払総額：　\(n x\)
  • 利息総額：　\(n x – M_0\)

利息率

借金返済における利息の大きさを知る上で重要になるのが『利息率』です。毎月定額返済を行う元利均等方式ですが、返済金額に対する利息の割合は毎月変化していきます。

実際に支払っている金額のうち何％が利息、すなわち手数料なのかがわかると、お金を借りるということに対するリスクをしっかりイメージすることができます。

それでは\(m\)回目の返済における利息率を計算してみます。\(m\)回目の利息は\((m-1)\)回目の支払い後に残った元金に対してかかります。それを月々の支払い金額で割ればいいので、

$$（m回目の支払いの利息率）= \frac{M_{m-1} p’}{x}$$

と表すことができます。ここで用いる\(x\)はすでに計算によって求めた定数であることに注意してください。

\(M_{m-1}\)は式(4)の\(n\)を\((m-1)\)に置換すれば求まります。従って、

$$（m回目の支払いの利息率）= (\frac{p’}{x} M_0 – 1)(1+p’)^{m-1} + 1$$

具体例で計算してみる

次のような具体例で計算してみましょう。

  • 借入総額：500万円
  • 返済期間：5年
  • 年利：3%

方程式に入れるために、与えられた数値の単位を変換します。まず返済期間5年というのは月に変換すると60カ月になります。また、年利3％を割合表示の月利に変換すると月利0.0025になります。

従って式(5)に代入する数字は、\(M_0 = 500\)万円、\(p’=0.0025\)、\(n=60\)です。実際に計算してみると月々の返済額\(x\)は、

$$ x \approx 89,844 \ 円$$

さらに、全期間における支払い金額と利息の総額は次のようになります。

  • 支払総額：5,390,640 円
  • 利息総額： 390, 640 円

500万円を金利3%で5年間借りると39万円の手数料がかかるんですね〜。結構大きい額になりました。さて、利息率はどうでしょうか。返済期間における利息率の推移を表すグラフを作ってみました。

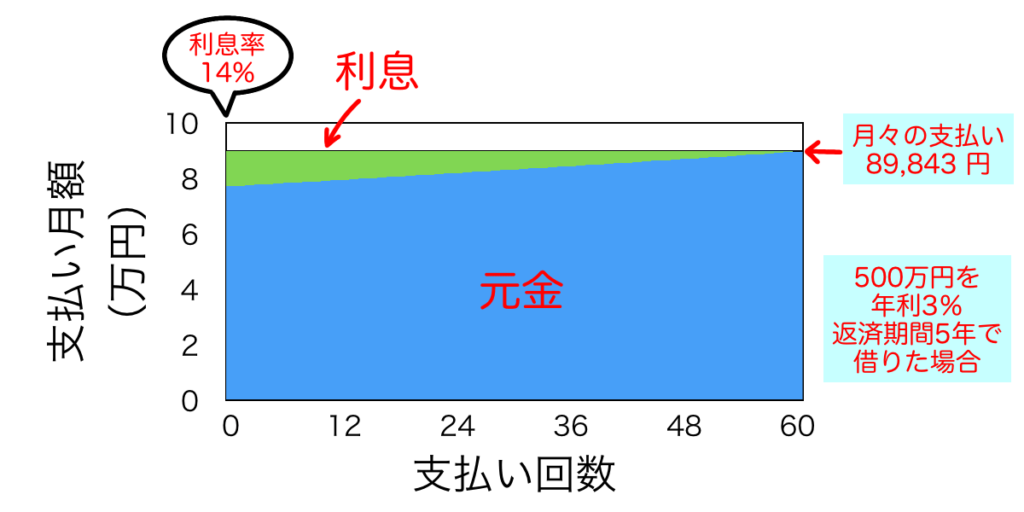
今回設定した条件では返済開始直後は利息率が約14％になります。月々の返済額は89,843円ですから、12,578円の手数料（利息）を支払っていることになります。

返済が定額のため、購入したものの価格を毎月定額で払っているような錯覚に陥りますが、かなりの金額の利息が含まれていることは常に意識しておいた方がいいでしょう。

まとめ

いかがでしたでしょうか。

元利均等方式での借金返済は高校数学で出てくる等比級数という考え方を使うとすぐに計算可能な方程式で表すことができました。

この方程式に借金の条件を代入して計算すれば、月々の返済額や利息率などが計算できます。これからローンを組むことを考えている方、もしくはローンの返済中の方は、一度この方程式を使って利息率を計算してみてはどうでしょうか？

最新情報をチェックしよう！

マネーの最新記事8件