前回の記事では振り子をモデルとして単振動では振動のエネルギー\(E\)と周波数\(\nu\)の比\(\frac{E}{\nu}\)が断熱不変量になっていることを導きました。一方、空洞輻射への熱エネルギーの分配関数を決めるためには、空洞内の温度\(T\)と周波数\(\nu\)を同時に含む断熱不変量が必要です。
本記事では熱力学的な考察を行い、単振動の断熱不変量を温度と振動数の断熱不変量に変換することを試みます。
空洞輻射の圧力
温度と振動数の断熱不変量を導く第一ステップとして、まずは空洞輻射において断熱不変量が生じる原因について考えていきます。
前回の記事で、振り子運動の類推から単振動における断熱不変量を導きました。
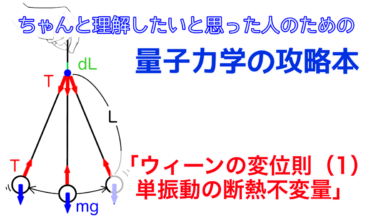
振り子が振動する周期よりも十分ゆっくり紐をたぐり寄せるとき、振り子の振動エネルギー\(E\)と振動周波数\(\nu\)の比が断熱不変量だったのです。
$$ \frac{E}{\nu} = 一定 $$このとき、断熱不変量が定義できたのは紐を引っ張る手がした仕事の一部が振り子の振動エネルギーを増加させ、これによって振り子の周波数も変化したからです。
振り子の紐をゆっくりたぐること、すなわち準静的な操作が単純に振り子全体の位置エネルギーを増加させる以上の仕事をしたのは、紐に働く張力が振り子の静的な重力\(mg\)だけでなく、重力の時間変化や遠心力などを含んでいたからです。
これら静的な重力以外の力は、振り子が紐を通して外界に対して押したり引いたりする力、すなわち圧力と考えることができます。
この振り子の圧力と反対方向に紐を引っ張り振り子に正の仕事をしたため振り子の振動エネルギーが増加したのです。
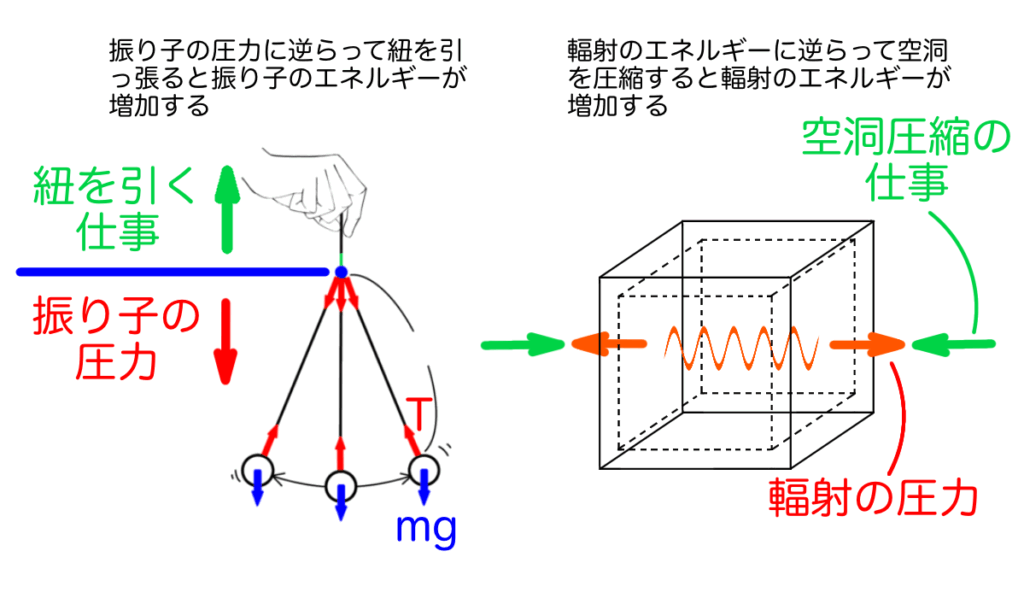
前の記事でも紹介した通り、エネルギー\(E\)と周波数\(\nu\)の比\(\frac{E}{\nu}\)が断熱不変量となっている振り子の場合、振動エネルギーと周波数の変化分を\(dE\)、\(d\nu\)と表すと次のような関係がありました。
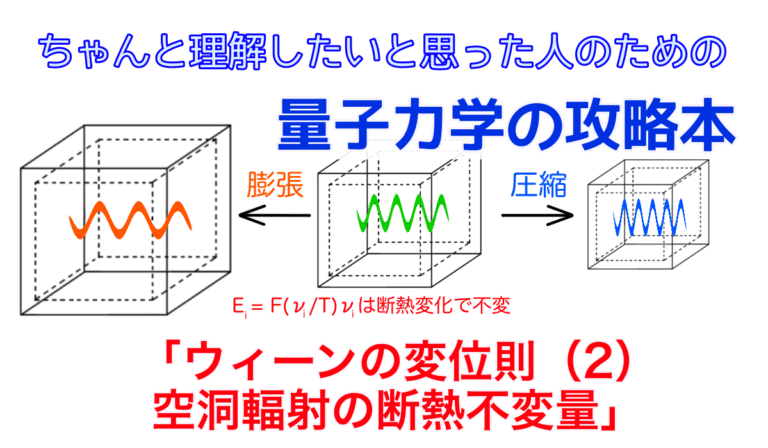
$$ \frac{dE}{E} = \frac{d\nu}{\nu} $$同様に空洞輻射が内壁に及ぼす圧力と、それに逆らって空洞を変形させた時の輻射のエネルギー変化の関係を導くことができます。今、空洞内に閉じ込められている周波数\(\nu_i\)、エネルギー\(E_i\)の電磁波について考えます。添字の\(i\)は電磁波を数えるための指標でモードと呼ばれることがあります。
準静的な変化に対するモード\(i\)の電磁波において、周波数とエネルギーの変化量に関する関係をもう一度書くと、
$$ \frac{dE_i}{E_i} = \frac{d\nu_i}{\nu_i}\tag{1} $$となります。一片の長さが\(L\)である立方体の空洞内に閉じ込められた電磁波の場合、周波数\(\nu_i\)は空洞内壁では電磁波の振幅が0になるという境界条件から、次のように離散的な値になるのでした(参考:レイリー・ジーンズの法則)。
$$ \nu=\frac{c}{2L}n_i\tag{2} $$ここで\(c\)は光速を表しています。\(n_i\)は電磁波のモードに対応する自然数で、3次元空間の場合は\(x\)、\(y\)、\(z\)方向に伝播する自由度があるので、それぞれの方向に対するモード番号を使って次のように計算できます。
$$ n_i=\sqrt{n_x^2+n_y^2+n_z^2} $$ただし、\(n_x\)、\(n_y\)、\(n_z\)は0以上の整数です。ここで、もう一度確認しておきますが、電磁波を特徴づける量は周波数\(\nu\)以外にも、角速度\(\omega\)や波長\(\lambda\)、波数\(k\)などがありました。これらは次のような関係式でつながっています。
$$ \nu_i=\frac{1}{2\pi}\omega=\frac{c}{\lambda}=\frac{c}{2\pi}k $$さて、話を元に戻して(2)式において\(\nu_i\)を\(L\)で微分すると、
$$ \frac{d\nu_i}{dL} = -\frac{1}{2}\frac{c n_i}{L^2} = -\frac{\nu_i}{L} $$ですから、
$$ \frac{d\nu_i}{\nu_i} = -\frac{dL}{L}\tag{3} $$となります。この(3)式を(1)式に代入すると電磁波のエネルギーを空洞の長さと関連付けることができます。
$$ \frac{dE_i}{E_i} = -\frac{dL}{L} $$さらに、今考えている準静的な空洞の変化において空洞の形が常に一片がLの直方体に保たれているとすると、その体積は\(V = L^3\)ですので、
$$ dV = 3L^2dL $$が求まります。従って、次のようにエネルギーと空洞の体積の関係がわかります。
$$ \frac{dE_i}{E_i} = -\frac{1}{3}\frac{dV}{V}\tag{4} $$さて、それでは実際に空洞の体積を断熱的にじわじわ変化させるときに必要な仕事と輻射が壁に及ぼす圧力の関係を求めてみましょう。空洞内に閉じ込められた電磁波の場合、振り子の時とは異なり重力を考える必要はありません。つまり、電磁波の各モードのエネルギー変化をすべて足し合わせたものが、空洞の大きさを変化させるのに必要な仕事になります。空洞輻射が外部にした仕事を\(dW\)とすると、
$$ dW = -\sum_i{dE_i}\tag{5} $$が成り立ちます。空洞輻射が外部に仕事をすると、輻射自体の内部エネルギーが減少するということですね。(4)式を(5)式に代入すると、
\begin{eqnarray} dW &=& \frac{1}{3}\frac{dV}{V}\sum{E_i}\\ \therefore \frac{dW}{dV} &=& \frac{1}{3}\frac{\sum{E_i}}{V}\tag{6} \end{eqnarray}ここで(6)式の左辺は仕事を体積で割っているので圧力\(P\)の次元を持ちます。また、右辺の\(\sum{E_i}/V\)は空洞輻射の全エネルギーを体積で割っているのでエネルギー密度\(\rho\)に他なりません。従って、輻射が空洞の6つの面に及ぼす圧力の平均値はエネルギー密度の\(\frac{1}{3}\)倍に等しいことがわかります。
$$ P = \frac{1}{3}\rho \tag{7} $$空洞輻射の二つ目の不変量(振動数と温度)
ここまでの計算で、空洞輻射が空洞内壁に及ぼしている圧力と、空洞の体積を断熱的に変化させたときに、輻射が外部にする仕事を定式化することができました。
ここでは、Stefan-Boltzmannの法則を適用し、空洞の体積を断熱的に変化させたとき、輻射の振動数と温度の比が、またもや不変量となっていることを示したいと思います。
Stefan−Boltzmannの法則は「黒体輻射のエネルギー密度は温度の4乗に比例する」というものです。この法則の導出については別の記事にて解説したいと思います。これを式にすると次のようになります。
ここでは空洞輻射の内部エネルギーの増減について考えるため、空洞が断熱圧縮、あるいは断熱膨張されたときに空洞輻射が外部から受ける仕事を考えます。この場合(6)式とは逆負号になるため、
\begin{eqnarray} \frac{dW}{dV} &=& -\frac{1}{3}\rho\tag{8} \end{eqnarray}となります。一方、熱力学的第一法則より系の内部エネルギー変化\(dU\)は、流入した熱量\(dQ\)と系が外部にした仕事\(dW\)を用いて、
$$ dU=dQ−dW $$と表すことができます。ここで断熱条件(\(dQ=0\))を考えていること、系が外部から受けた仕事を考えているため\(dW\)の符号が反転すること、さらに内部エネルギーの変化が\(dU=d(\rho V)\)と表せることに気を付けると、\(dW=d(\rho V)\)が成り立ちます。したがって、(8)式は次のように計算できます。
\begin{eqnarray} \frac{d(\rho V)}{dV} &=& -\frac{1}{3}\rho\\ \therefore \frac{d(\rho V)}{\rho V} &=& \frac{1}{3}\frac{dV}{V}\\ \therefore \ln |\rho V| &=& \frac{1}{3}\ln |V| + C\\ \therefore \ln |\rho V^{\frac{4}{3}}| &=& C\\ \therefore \rho V^{\frac{4}{3}} &=& C^e = A\\ \therefore \rho &=& \frac{A}{V^{\frac{4}{3}}}\\ \end{eqnarray}つまり、断熱変化の際に、空洞内のエネルギー密度と体積の間には、
\begin{eqnarray} \rho ∝ \frac{1}{V^{\frac{4}{3}}} \end{eqnarray}という関係が成り立ちます。したがって、Stefan-Boltzmanの法則より、
\begin{eqnarray} T ∝ \frac{1}{V^{\frac{1}{3}}}\tag{9} \end{eqnarray}であることがわかります。すなわち、空洞輻射の温度は空洞の体積の立方根に反比例して変化するという結論が得られます。
一方、(3)式の両辺を積分し、\(L=V^3\)を用いると、
\begin{eqnarray} \int{\frac{d\nu_i}{\nu_i}} &=& -\int{\frac{dL}{L}}\\ \therefore \ln{\nu_i} &=& -\ln{L}+C\\ \therefore \nu_i L &=& e^C\\ \therefore \nu_i &\propto& L^{-1}\\ \therefore \nu_i &\propto& V^{-1/3}\tag{10}\\ \end{eqnarray}という関係が求まります。従って、(9)式、(10)式より直ちに
$$ \frac{\nu_i}{T} = 一定 $$が求まり、空洞輻射の各モードの振動数と温度が断熱不変量になっていることがわかります。
ウィーンの変位則
いよいよウィーンの変位則を導くための準備が整いました。私たちはこれまでの議論で、空洞の大きさをじわじわ、断熱的に変化させる際に二つの不変量が存在することを突き止めました。
その二つの不変量とは輻射の各モードにおけるエネルギーと振動数の比\(E_i/\nu_i\)、および振動数と輻射の温度の比\(\nu_i/T\)でした。
ここでもう一度、空洞輻射問題はどんな問題だったかに立ち返ると『ある温度Tの空洞から出てくる光のスペクトルはどのような形状か?』という命題でした。スペクトルとは横軸が周波数(あるいは波長)で縦軸がエネルギー(あるいは光の輝度)のグラフのことですので、空洞輻射の各モードを周波数\(\nu_i\)で指標付けし、その各々に空洞内の熱エネルギーがどのように分配されるか、すなわち、
$$ E_i = f(\nu_i) $$における分布関数\(f(\nu_i)\)を突き止めることが空洞輻射問題の解決に相当します。レイリー・ジーンズらの考察によれば、古典的な等分配の法則に基づき\(E_i=k_B T\)を仮定して式を展開したものの、実際の実験結果を説明する式は得られませんでした。
ウィーンの考察によって得られた二つの断熱不変量を用いても、この問題を完全に解決するには至りませんが、非常に重要な知見を引き出すことができます。上の式で用い分布関数\(f(\nu_i)\)は一般には空洞の温度によって様々な関数をとる可能性があります。しかし、空洞体積の断熱変化によって\(E_i/\nu_i\)、および\(\nu_i/T\)が不変であるというのであれば、分布法則を、
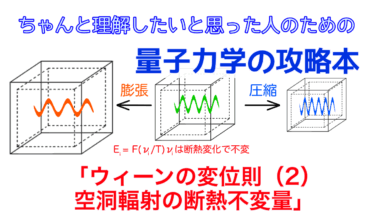
$$ \frac{E_i}{\nu_i} = F\left( \frac{\nu_i}{T} \right) $$という形に書いておけば関数\(F(x)\)はもはや系の温度に関係しないはずです。以上より、空洞輻射におけるウィーンの変位則の最終的な形が下記のように求まります。
$$ E_i = F\left( \frac{\nu_i}{T} \right)\nu_i\tag{11} $$ウィーンの変位則は空洞輻射の完全な理解には届かないものの、大変重要な知見を与えてくれます。本記事においても明らかになったように、空洞の体積を断熱的に変化させていくと、空洞内の温度もそれに伴って変化します。すなわち、ある一つの温度Tにおいて空洞輻射を測定しスペクトル形状が明らかになれば、(11)式を用いて他のどの温度のスペクトルも予想できることになります。このウィーンの変位則は実験結果と完全に一致し、空洞輻射問題の解決に大きく貢献することになります。
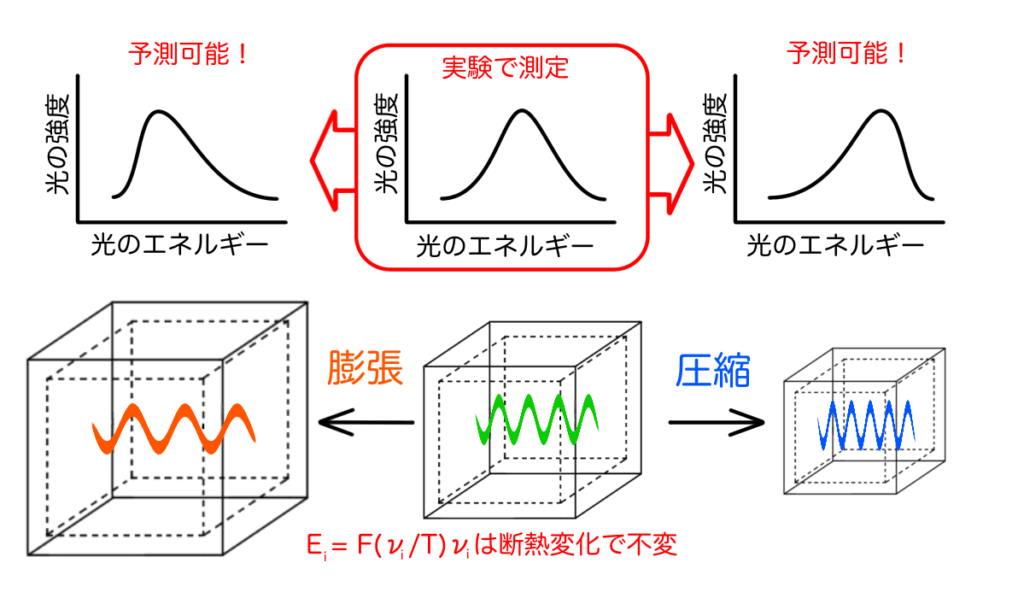
さらに、これまで手探りだった空洞輻射問題が、分布関数\(F(\frac{\nu_i}{T})\)はどんな形をとるのか、という問題に帰結することを示したのもウィーンの大きな功績だったといえます。このウィーンの変位則を足掛かりに、空洞輻射問題の完全解決、そして量子力学の幕開けに向けてプランクが満を持して登場してくるのです。
まとめ
皆さんいかがでしたでしょうか? 本記事では空洞輻射が外部に与える圧力を定義し、そこから二つ目の断熱不変量である\(\nu_i/T\)を導きました。さらに、空洞輻射の断熱変化における二つの不変量から、ウィーンの変位則を導きました。
空洞輻射問題の完全解決には至らなかったものの、ウィーンの貢献は空洞輻射問題の核心をあらわにし、より深い物理的考察を可能にしました。
次の記事では、いよいよ量子力学の偉人、プランクが登場します。空洞輻射問題の完全解決、そして量子力学の夜明けはすぐそこまで迫っています。
ここまでお読みいただき、どうもありがとうございました。次の記事もぜひ楽しみにしていてください。