1900年にレイリーは空洞内の電磁波の自由度に対して等分配の法則が成立すると仮定し、黒体輻射のスペクトルに関する理論を発表しました。時系列的には黒体輻射に関するヴィーンの変位則の方が先に発表されていましたが、ヴィーンの考え出した輻射スペクトルの理論式は物理的な根拠が乏しく、黒体輻射問題の解決には至っていませんでした。レイリーは当時成功を収めていた統計力学の考え方を黒体輻射問題に適用し、空洞内部の電磁波の自由度に対して等分配の法則が成り立つとして輻射スペクトルの理論式の導出を試みたのです。
はい、こちらがレイリーさんです。1842年にイギリスの貴族の家系に生まれ、本名はジョン・ウィリアム・ストラットと言います。後に第3代のレイリー男爵となり物理学者としてもノーベル賞を含む多大な功績を残された方なので、レイリー卿というときはこの第3代レイリー男爵を指すことが多いようです。ちなみに、よく晴れた日に空が青く見える理由を発見したのもこのレイリーさんです。
一方で、レイリーが1900年に発表した輻射法則は誤りを含む不完全なものでした。これを後でジェームス・ジーンズが修正したため、レイリー・ジーンズの輻射法則という名前がついています。ジーンズさんは輻射に関する理論はもとより、天文学の分野でも多くの功績を残されています。ジーンズさんの写真も載せておきましょう。
彼ら2人によって作られたレイリー・ジーンズの輻射法則は古典力学に立脚しており、その導出過程は完全に正しいものの、黒体輻射問題を解決する事はできませんでした。このことは黒体輻射という現象が古典物理学の範疇を超えた現象である可能性を示唆していました。古典と量子の決定的な違いを理解する上でも、このレイリー・ジーンズの輻射法則を眺めることは大変有意義です。それでは統計力学における等分配の法則とはどのような考え方なのかを見ていくことにしましょう。
力学系の自由度と等分配の法則
当時、統計力学の分野では無数に存在する気体分子の運動を統計的に扱うことによって気体の体積や温度、圧力などのマクロで計測可能な量を関連性を定式化することに成功していました。その根幹をなす考え方が熱エネルギーは力学系の各々の自由度に対して均等に分配されるという等分配の法則でした。
例えば、ヘリウムやアルゴンのような原子一つで自由に空間を飛び回る単原子分子の気体では、3次元空間の中を自由に飛び回ることができるので、分子一つあたりの自由度は3とカウントされます。これに対して酸素や窒素などの２つの原子が結びついて一つの分子を構成する2原子分子の期待では、先ほどの自由度3に加えて、回転という自由度が二つ加わることになるので、自由度は5ということになります。等分配の法則では、これらの自由度に対して熱的なエネルギーが均等に分配されることを仮定して、気体分子の持つエネルギーを統計的に扱うことで気体全体の圧力や体積などを正確に計算することに成功しました。
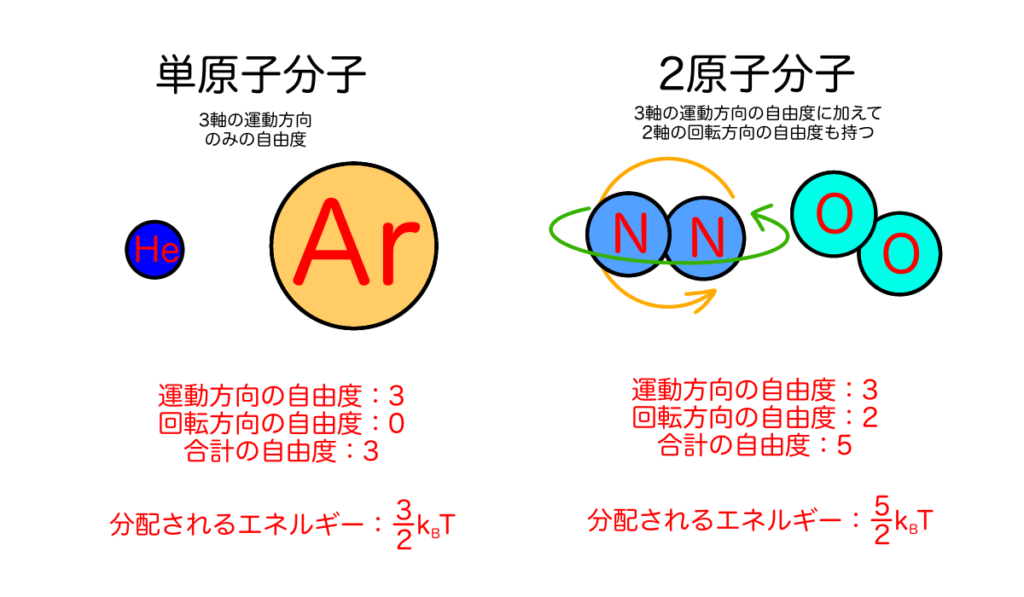
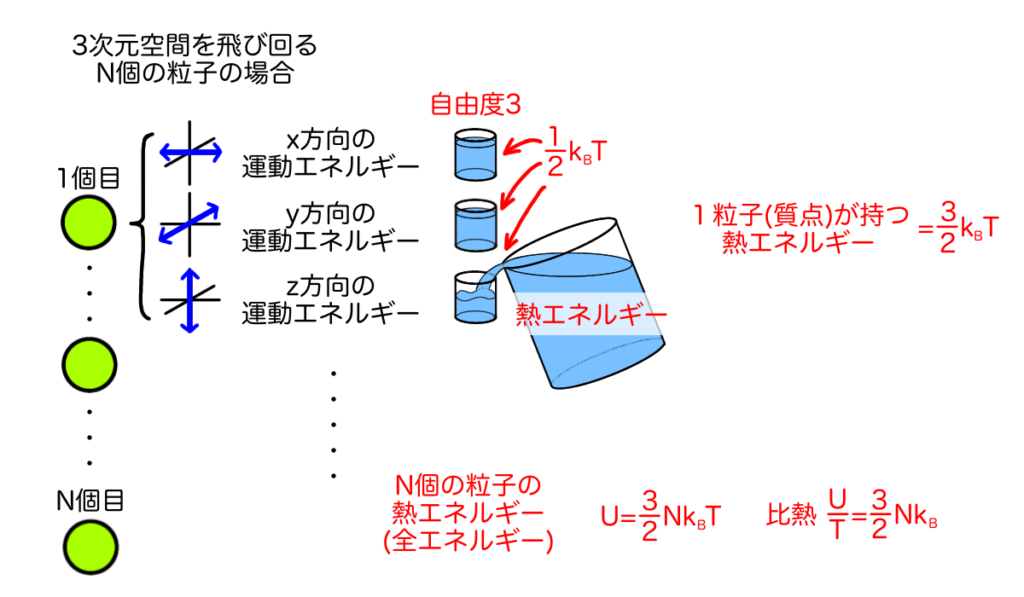
熱力学的な考察から、等分配の法則により温度\(T\)にある系では1つの自由度あたり\(\frac{1}{2}k_BT\)のエネルギーが分配されます。\(k_B = 1.38 \times 10^{-23} \mathrm{[J/K]}\)はボルツマン定数です。例えば、温度20℃にあるヘリウム原子は3次元空間を自由に飛び回る時の自由度が3なので、ヘリウム原子1こあたりに分配されるエネルギーは\(\frac{3}{2}k_BT\)ということになります。この考え方を用いると、単原子分子の比熱の実験結果を極めて正確に再現できることがわかっていました。
レイリーとジーンズはこの等分配の法則を黒体輻射問題に適用し、輻射のエネルギー密度を理論的に導きました。彼らは黒体輻射を空洞輻射問題に焼き直し、空洞の中に存在する電磁波がどれくらいの自由度を持つかを考えることで、輻射スペクトルを予測しようと試みたのです。結論から述べると、この試みは黒体輻射の説明には成功しませんでした。一方で、古典的な描像では黒体輻射問題を解決できないことが鮮明になり、新たな理論の構築が必要であることが広く認識されたことは物理学の発展を考える上ではとても重要だったと言えます。さて、ここでは古典物理学の限界を鮮明にしたレイリー・ジーンズの輻射法則の導出について具体的に考えていきましょう。
空洞内における電磁波の自由度
まずは空洞内に充満する電磁波の自由度を数えてみましょう。電磁波は言葉通り電場と磁場が交互に振動しながら空間を伝搬していく波のことで、3次元の自由空間を伝搬する電磁波の電場成分は3次元の空間座標\(\mathbf{r} = (x, y, z)\)に時間\(t\)を加えた4変数の関数で表すことができます。この電場\(\mathbf{E}(\mathbf{r},t)\)が真空中を伝搬するときのふるまいは次の方程式によって記述されます。
$$ \nabla^2 \mathbf{E} – \varepsilon_0 \mu_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0 $$この方程式は電磁波の満たす波動方程式で、マクスウェル方程式から簡単に導かれます。上式において誘電率\(\varepsilon_0\)と透磁率\(\mu_0\)の積は電磁波の進む速度\(c\)と次のような関係があります。
$$ c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}} $$この値を計算してみると、
$$ \varepsilon_0 = 8.854 \times 10^{-12} \mathrm{[F/m]} \\ \mu_0 = 1.257 \times 10^{-6} \mathrm{[N/A^2]} $$なので、\(\frac{1}{\sqrt{\varepsilon_0 \mu_0}} = 2.998 \times 10^8 \mathrm{[m/s]}\)となって、よく知られている秒速30万キロメートルという光の速度と同じになります。つまり、電磁波を記述するための波動方程式から光の速度が自動的に出てくるため古典物理学において光の正体が波であると決定づけられたのです。
真空中における電場の方程式を光速\(c\)を使ってもう一度書くと次のようになります。
$$ \nabla^2 \mathbf{E} – \frac{1}{c^2} \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0 \tag{1} $$この波動方程式は電磁気学や流体力学、そして量子力学でも頻繁に登場する微分方程式です。様々な関数が解になり得ますが、ここでは波の等位相面が平面になる、いわゆる平面波解を考えることにします。波動方程式の平面波解は次のような形をしています。
$$ \mathbf{E}(\mathbf{r},t) = E_0 \sin (\mathbf{k \cdot r}) \cos (\omega t + \alpha) $$この関数を(1)式に代入すれば、解になっているかどうかをすぐ確かめることができます。新しく出てきた文字について、\(E_0\)が任意の電場振幅、\(k\)が電場の波数、\(\omega\)が電場の角周波数を、そして\(\alpha\)は任意の位相因子を表しています。特に電磁波の伝搬速度を\(c\)としたとき、\(c = \omega / k\)という関係で波数と角周波数は繋がっています。
この平面波解は自由空間を時間と空間に対して振動しながら伝搬していく波を記述する関数です。空洞の中の閉じ込めを再現するために境界条件を導入しましょう。
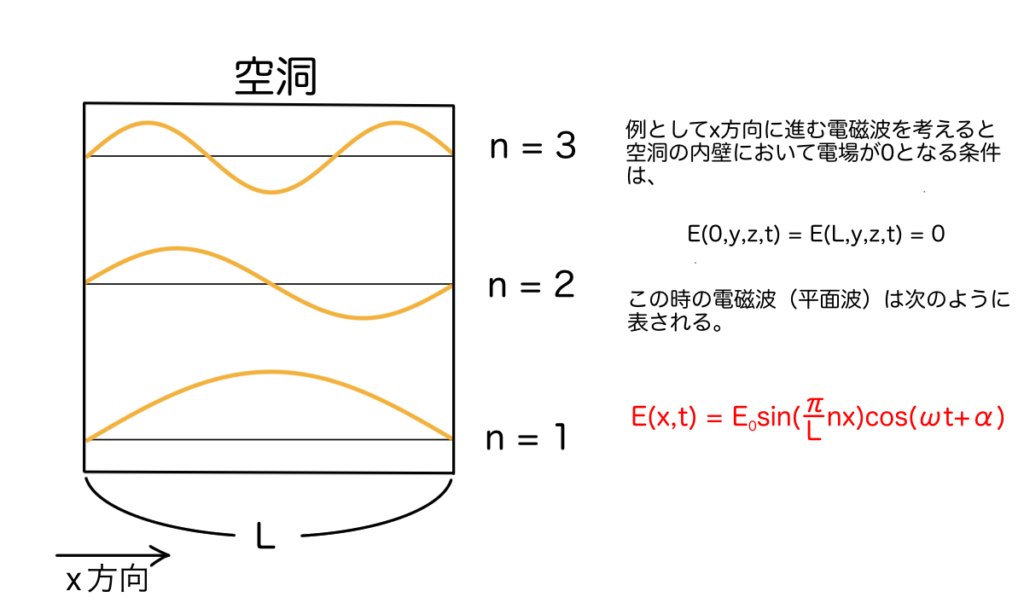
一辺の長さが\(L\)の立方体の空洞の中に電磁波が閉じ込められているとすると、壁の上では電磁波の振幅は0でなくてはなりません（もし電磁波が壁を透過できる場合は壁の中でも電磁波は有限の振幅を持つことが許されます）。この境界条件を式で表すと次にようになります。
$$ E(0, t) = E(L, t)=0 $$上式では空間変数をスカラーのように描きましたが、当然全ての方向に等価な境界条件を導入します。この境界条件によって電磁波の波長が\(L\)のちょうど整数倍になる成分しか存在できなくなります。従って、波数\(k\)が次のように変更されます。
$$ \mathbf{E}(\mathbf{r},t) = E_0 \sin (k_x x + k_y y + k_z z) \cos (\omega t + \alpha) $$ $$ \mathbf{k}=(k_x,k_y,k_z) \\ k_x = \frac{n_x \pi}{L},\quad k_y = \frac{n_y \pi}{L},\quad k_z = \frac{n_z \pi}{L} $$\(n_i (i=x, y, z)\)は正の整数であり、それぞれの座標軸に沿って\((n_i-1)\)個の節を持つことを意味しています。また、3次元空間における電磁波の状態は\((k_x, k_y, k_z)\)をひと組のパラメータとして指定され、「モード」と呼ばれることがあります。さらに各モードには電磁波が横波であることに由来した偏光の自由度が存在し、一つのモード当たり自由度を2つずつ持っています。
例えば\((n_i \le 2)\)であるような電磁波の集合体は次のとおり全部で27個のモードを内包します。
$$ (0,0,0),\quad(0,0,1),\quad(0,0,2)\\ (0,1,0),\quad(0,1,1),\quad(0,1,2)\\ (0,2,0),\quad(0,2,1),\quad(0,2,2)\\ (1,0,0),\quad(1,0,1),\quad(1,0,2)\\ (1,1,0),\quad(1,1,1),\quad(1,1,2)\\ (1,2,0),\quad(1,2,1),\quad(1,2,2)\\ (2,0,0),\quad(2,0,1),\quad(2,0,2)\\ (2,1,0),\quad(2,1,1),\quad(2,1,2)\\ (2,2,0),\quad(2,2,1),\quad(2,2,2) $$従って、このような電磁波の集合体には全部で54の自由度が存在することになります。実際に扱う空洞の長さ\(L\)は電磁波の波長と比較して極めて大きいため空洞輻射における電磁波の自由度はもっと巨大な値を取ることになると思われます。なぜなら\(\frac{n_i \pi}{L}\)を満たすような\(n_i\)は途方もない数になるからです。
さて、結局空洞の中に閉じ込められた電磁波の自由度を数えることは、波数空間において\((k_x, k_y, k_z)\)のセットが何個あるかを数えることに相当します。波数空間とは我々が3次元空間を考える時に使う座標軸\(x, y, z\)軸を波数に直して、\(k_x, k_y, k_z\)軸にしたものです。量子力学でも極めてよく出てくる図なので慣れておくと大変便利です。
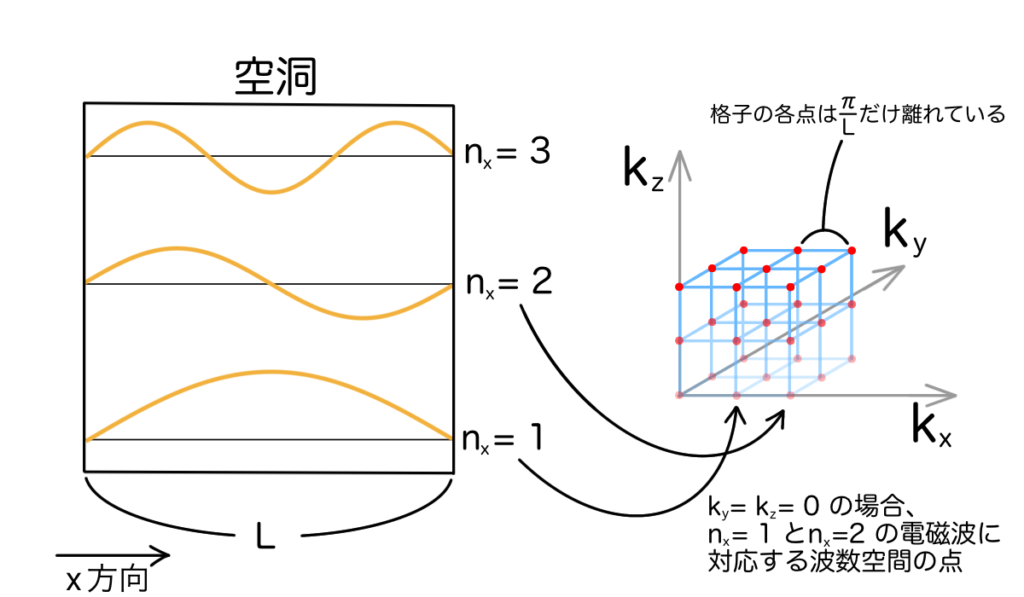
この波数空間においてモードを指定する\((k_x, k_y, k_z)\)のセットは一つの点として描くことができます。点と点の間隔は\(\frac{\pi}{L}\)だけ離れています。従って、波数空間における一つのモードが占める体積は\( { \left( \frac{\pi}{L} \right) }^3\)ということになります。
一方、ある波数\(k\)を持った電磁波の自由度を考えたい場合、\(k\)とそこから微小波数\(dk\)だけ増加した\(k+dk\)の範囲にあるモードを数えればいいことになります。この領域は3次元の波数空間における球殻を第1象限だけ切り取った体積に相当します。
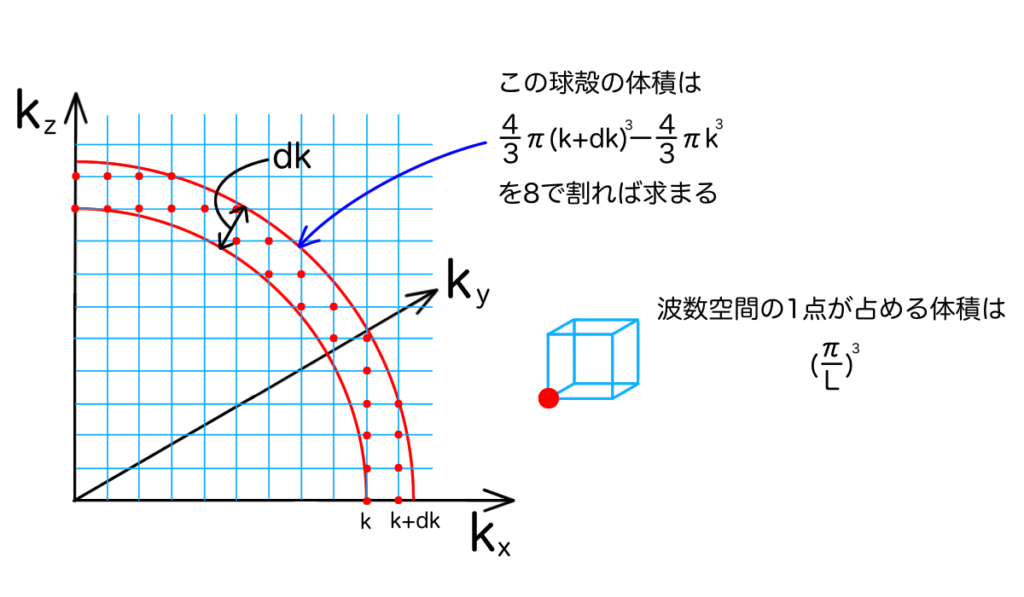
この球殻の体積は半径\((k+dk)\)の球の体積から半径\(k\)の球の体積を引いて、それを\(\frac{1}{8}\)倍すれば求まります。
\begin{eqnarray} \require{cancel} \frac{1}{8} \left( \frac{4 \pi (k + dk)^3}{3} – \frac{4 \pi k^3}{3} \right)&=& \frac{\pi}{6} \left( 3 k^2 dk + \bcancel{3 k dk^2} + \bcancel{dk^3} \right)\\ &=&\frac{\pi}{2}k^2dk \end{eqnarray}上式に出てくる2次以上の微小項、すなわち\(dk^2\)と\(dk^3\)を含む項を無視すれば\(\frac{\pi}{2}k^2dk\)が得られます。これを先ほどの1モードが占める体積\(\left(\frac{\pi}{L}\right)^3\)で割ることで球殻の中に含まれるモードの総数を計算することができます。
\begin{eqnarray} (球殻に含まれるモード数) &=& \frac{\pi}{2}k^2dk { \left( \frac{L}{\pi} \right) }^3 \\ &=& \frac{L^3}{2\pi^2}k^2dk \end{eqnarray}さらにモードの数に偏光の自由度2をかけることで波数\(k\)の電磁波が持つ自由度をになります。
\begin{eqnarray} (波数kの電磁波が持つ自由度) = \frac{L^3}{\pi^2}k^2dk \end{eqnarray}等分配の法則を仮定したときの輻射のエネルギー密度
統計力学によれば電磁波の各自由度に対して熱エネルギーは\(k_BT\)ずつ、均等に分配されます。ここで\(k_B=1.38 \times 10^{-23} \mathrm{[J/K]}\)はボルツマン定数です。
従って、先ほど求めた電磁波の自由度に\(k_BT\)をかけると温度\(T\)において波数\(k\)の電磁波が持つエネルギーが求まります。
\begin{eqnarray} (温度Tにおいて波数kの電磁波が持つエネルギー) = \frac{L^3}{\pi^2} k_B T k^2dk \end{eqnarray}さらにこれを空洞の体積\(L^3\)で割ることによって空洞輻射のエネルギー密度\(\rho (T, k)\mathrm{[J/m^3]}\)を求めることができます。
\begin{eqnarray} \rho (T,k) = \frac{k_B T}{\pi^2} k^2dk \end{eqnarray}電磁波を特徴づけるパラメータとして空間的にどのくらいの頻度で振動するかを表す波数\(k\)は大変便利です。一方で電磁波は皆さんもご存知の通り角速度\(\omega\)や振動数\(\nu\)、そして波長\(\lambda\)でも特徴づけることができます。それらの関係をまとめると次の式で表すことができます。
\begin{eqnarray} k = \frac{\omega}{c} = \frac{2 \pi \nu}{c} = \frac{2 \pi}{\lambda} \end{eqnarray}空洞輻射のエネルギー密度も電磁波の\(\omega\)、\(\nu\)、\(\lambda\)で表すことができます。\(\omega\)、\(\nu\)については波数\(k\)の定数倍なので次のように簡単に換算できます。
\begin{eqnarray} \rho (T,\omega) &=& \frac{k_B T}{\pi^2 c^3} \omega^2d\omega\\ \rho (T, \nu) &=& \frac{8 \pi k_B T}{c^3} \nu d\nu \end{eqnarray}ただし波長\(\lambda\)については波数\(k\)の逆数になっているため微少量\(dk\)の変換に多少注意が必要です。\(k = \frac{2 \pi}{\lambda}\)であるから関数\(k\)の\(\lambda\)による微分は
$$ \frac{d k}{d\lambda} = – \frac{2\pi}{\lambda^2} $$となります。従って次のように温度\(T\)における波長\(\lambda\)の空洞輻射のエネルギー密度\(\rho (T, \lambda)\)は求まります。
\begin{eqnarray} \rho (T, \lambda) = – \frac{8 \pi k_B T}{\lambda^4} d\lambda \end{eqnarray}一見するとこの式はエネルギー密度が負の値になってしまっているように思えますが、これは積分方向の違いを反映しているためです。元々の式はある周波数の微小範囲\(d\nu = \nu_2 – \nu_1\)（ただし\(\nu_2 > \nu_1 \)）の中にある電磁波の自由度を数え上げてたわけですが、これを波長に変換するときには\(d\lambda = \lambda_2 – \lambda_1\)（ただし\(\lambda_2 < \lambda_1\)）となり積分範囲の大小関係が逆転するため負の符号が付いて相殺されているのです。
さて、ようやく古典物理学を駆使してレイリー・ジーンズの輻射法則に辿り着くことができました。この空洞輻射が持ちうるエネルギー密度をを実際に実験で計測可能な表面輝度に換算すると次のようになります。
$$ J_0[\mathrm{J/s \cdot m^2 \cdot sr}] = \frac{c k_B T}{\lambda^4} d\lambda $$この表面輝度に関する詳細な説明は一つ前の記事で説明していますので、興味のある方はぜひご参照ください。
産業革命が進むイギリスにおいて、製鉄業の発展に伴い高温になった鉄の温度と、そこから発せられる光の色との関係が注目されるようになりました。当時の古典物理学にを用いた考え方では、この温度と光の色の関係を説明することができませんでした。これがい[…]
レイリー・ジーンズの輻射法則は一目見て、現実に即していないことが明らかです。どんなに低くても有限の温度\(T\)を持つ空洞からは、波長\(\lambda\)が短くなればなるほど、\(\frac{1}{\lambda^4}\)倍に比例して強烈な電磁波が出てくることになります。電磁波の波長はどこまでも短くできるので、どんな空洞輻射を考えても最終的には無限大の強さの、超短波長の電磁波が出てくることになります。これでは空洞輻射として考えることのできる溶鉱炉の近くで作業している人たちは、たちまち大量のX線に被曝されて製鉄どころではないでしょう。いや、ありとあらゆる物体がX線を撒き散らしまくってしまうことにもなりかねません。
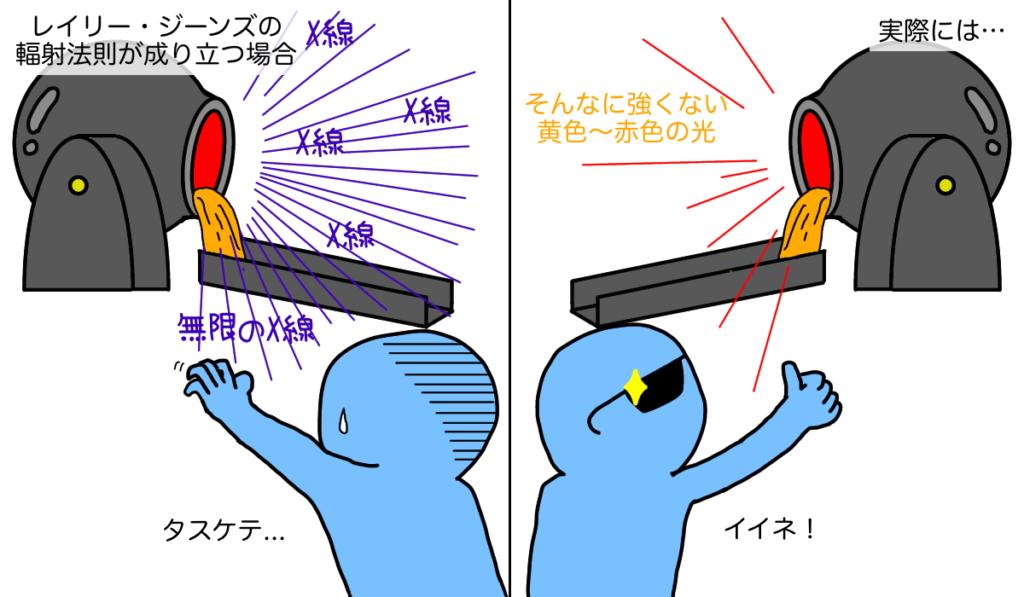
でも現実はそうなっていないことは周知の事実。このようにして、古典物理学による空洞輻射問題の解決が困難である事が明らかとなってきました。レイリーとジーンズが古典物理学による考察を進めるのと時を前後して、熱力学的に基づいたウィーンの考察、そしていよいよ量子力学の誕生とでもいうべきプランクの輻射法則が誕生します。古典物理では解決できなかった問題を、どのようなアイディアで克服していったのか、気になるお話は次回へ続きます。
