黒体輻射問題に対して熱エネルギーの等分配の法則を用いたレイリー・ジーンズの輻射法則では実験結果の説明が困難であることがわかり、古典物理学の限界があらわになりました。それでは黒体からの輻射スペクトルはどんな物理法則によって支配されているのでしょうか。
これを考える手がかりを与えていたのが1893年に提唱されたウィーンの変位則です。ウィーンは熱力学を駆使した巧みな考察から、黒体輻射の完全な解明ではないけれど、そのスペクトルがどのような関数系に従うべきか、という道筋を明らかにしました。のちに、このウィーンの変位則を足がかりとしてプランクが黒体輻射問題の正しい結論を導いているため黒体輻射問題の解決に対するウィーンの功績は極めて重要であると言えます。実際にウィーンには1911年に熱輻射の諸法則に関する発見に対してノーベル賞が贈られています。はい、ウィーンさんはこんな方です。

ウィーンの変位則の考え方を理解するには空洞内に閉じ込められた電磁波を一種の単振動とみなして、いくつかの熱力学的考察を行う必要があります。少し長い道のりになりますので、3つの記事に分けて紹介していきたいと思います。
一番目の本記事ではウィーンの変位則の基本となる断熱不変量という概念について説明するために単振動の代表とも言える振り子を取り上げます。さて、それでは黒体輻射問題を解決するための礎となった、ウィーンの変位則への扉を開きましょう。
ウィーンのアイディア
レイリー・ジーンズの輻射法則は、空洞内に満たされている様々な振動数をもつ電磁波に対して、均等に\(k_B T\)ずつ熱エネルギーが分配されているという仮定から導かれました。これは振動数\(\nu\)の電磁波に分配されるエネルギーを\(E_{\nu}\)と表すと、
$$ E_\nu = k_B T $$という式で表せます。この仮定に基づいて考えると、光の振動数はどこまでも大きくなることが出来る(言い換えると光の波長はどこまでも小さくなれる)ので振動数の大きな領域では空洞輻射も無限に大きくなってしまい、結局現実の実験結果を説明することはできませんでした。
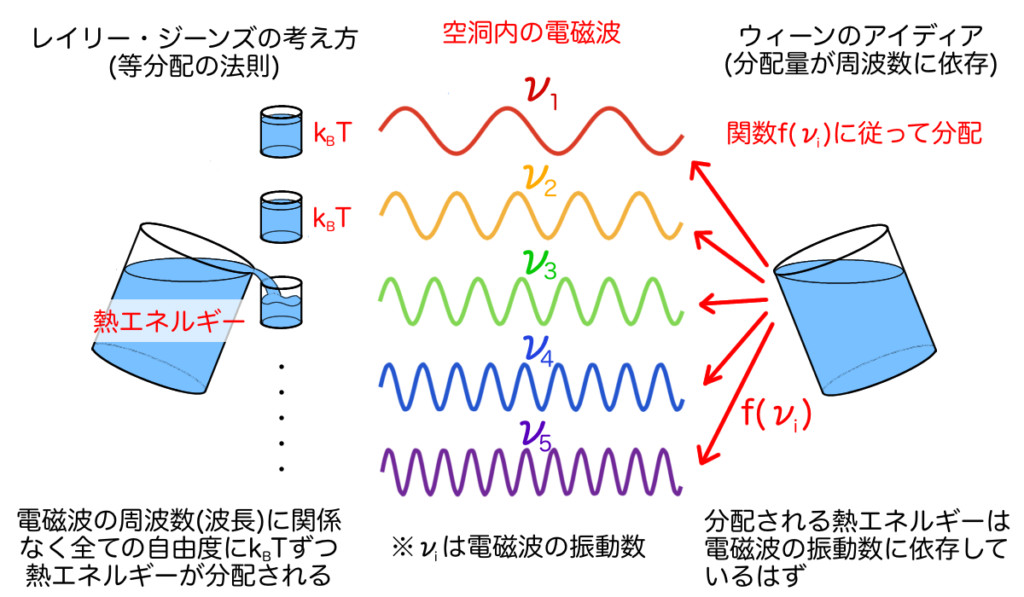
そこでウィーンは周波数で特徴づけられる電磁波に分配されるエネルギーもまた、周波数に依存するだろう、と考えました。つまり、
$$ E_\nu(\nu) = f(\nu) $$となるような関数\(f(\nu)\)があるはずだと考えたのです。一方で、1859年にグスタフ・キルヒホフはある波長(つまり振動数)における空洞輻射の強度は、物質の詳細によらず温度のみで決まる、ということを証明しています。当然ですが、熱エネルギーを様々な周波数の電磁波に分配する量は、その大元となる空洞の温度にも依存するはずです。ということは未知の分配関数は温度の関数\(f(\nu, T)\)でなくてはなりません。
当時の物理学では、この\(f(\nu, T)\)を完全に決定することはできませんでしたが、それでもウィーンは熱力学的な考察によって\(f\)は電磁波の周波数\(\nu\)と温度\(T\)で表される断熱不変量の関数であることを突き止めました。この断熱不変量はウィーンの変位則の中心となる重要な概念です。
断熱不変量というのは、ある周期運動をしている系の外部パラメータを、その周期運動の周期よりもず〜っとゆっくり変化させたとき、常に一定に保たれる量のことです。ウィーンは黒体輻射のスペクトルを断熱不変量の関数とみなすことで、ある特定の温度におけるスペクトルさえわかってしまえば、その他の温度の時のスペクトルも求めることができるという結論に辿り着きました。それでは断熱不変量のイメージを掴んでいただくために、振り子の運動を思い出してみましょう。
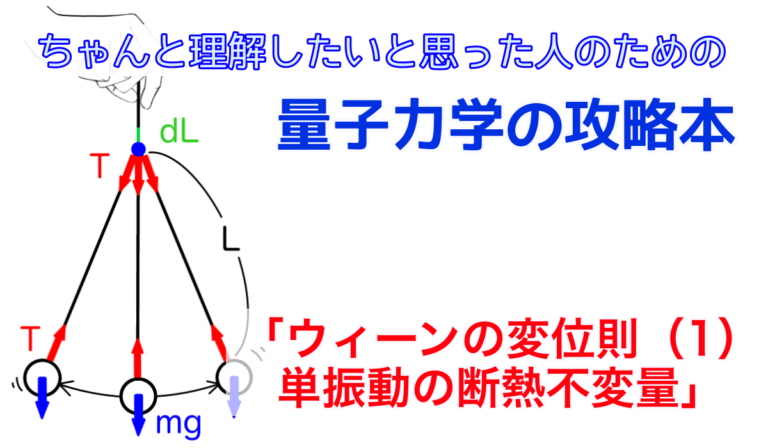
振り子の運動と紐の張力
ここに質量\(m\)の重りが長さ\(L\)の紐にぶら下がった振り子があります。手でこの重りを少し持ち上げてから離すと、重りはぶら〜んぶら〜んと揺れ始めます。この時、振り子が揺れる周期よりも十分ゆっくり紐を引っ張っていくと重りの運動にはどのような変化が起こるでしょうか?
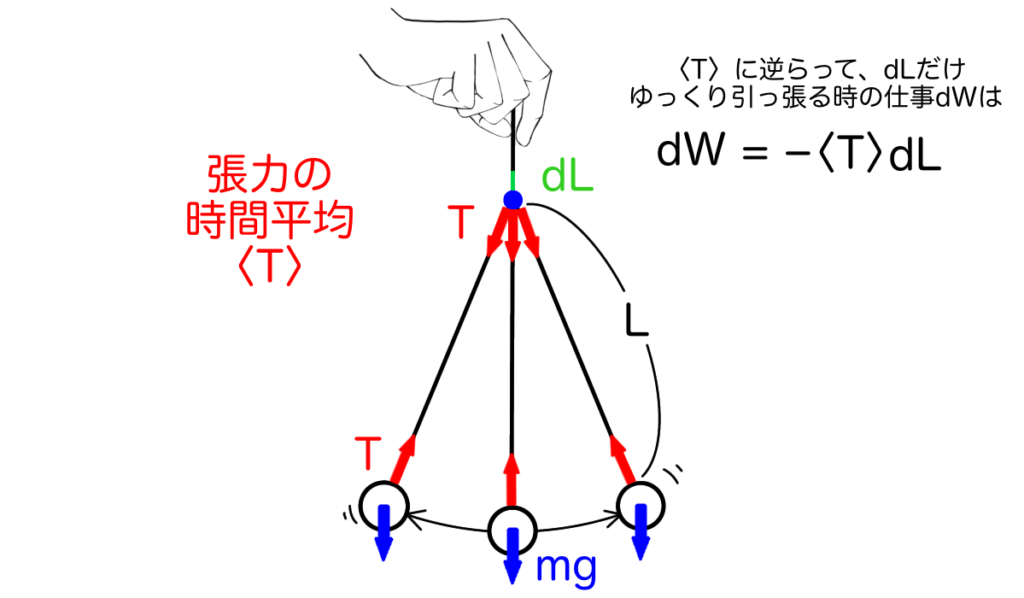
紐の両端にはちょうど同じ大きさで反対向きの張力\(T\)が働いています。この張力\(T\)に逆らって、振り子の紐を長さ\(dL\)だけ引っ張るということは、重りに対して\(dW = \: – \langle T \rangle dL\)だけの仕事をすることに相当します。当然、振り子が獲得するエネルギーはこの仕事に等しいはずです。ここで、張力\(T\)が\(\langle \quad \rangle\)で囲まれているのは時間平均を表すためです。また、仕事\(dW\)にマイナスがついているのは紐を引っ張る向きと張力が逆方向であることを表しています。それでは実際に張力\(T\)を具体的な関数として求め、そこから断熱不変量を見つけてみましょう。
重りのついている紐の先端に着目してください。張力\(T\)の源となるのは重りに働く重力と振り子の運動がもたらす遠心力です。
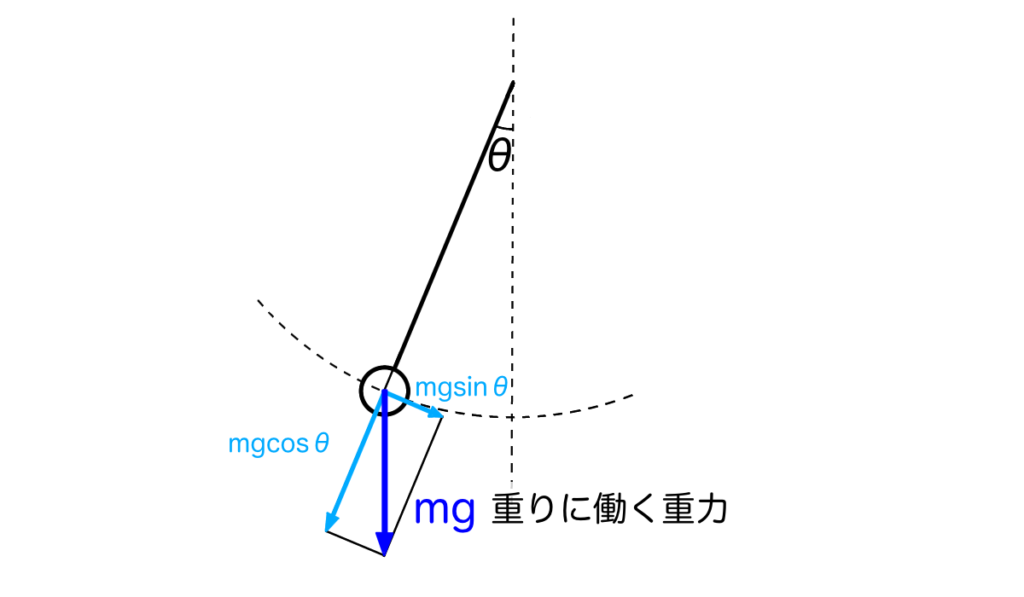
まず、重力について考えましょう。上の図のように質量\(m\)の重りに働く重力\(mg\)は動径方向の成分\(mg \cos \theta\)と角度方向の成分\(mg \sin \theta\)に分解できます。このうち、動径方向の成分のみが張力の発生に寄与します。
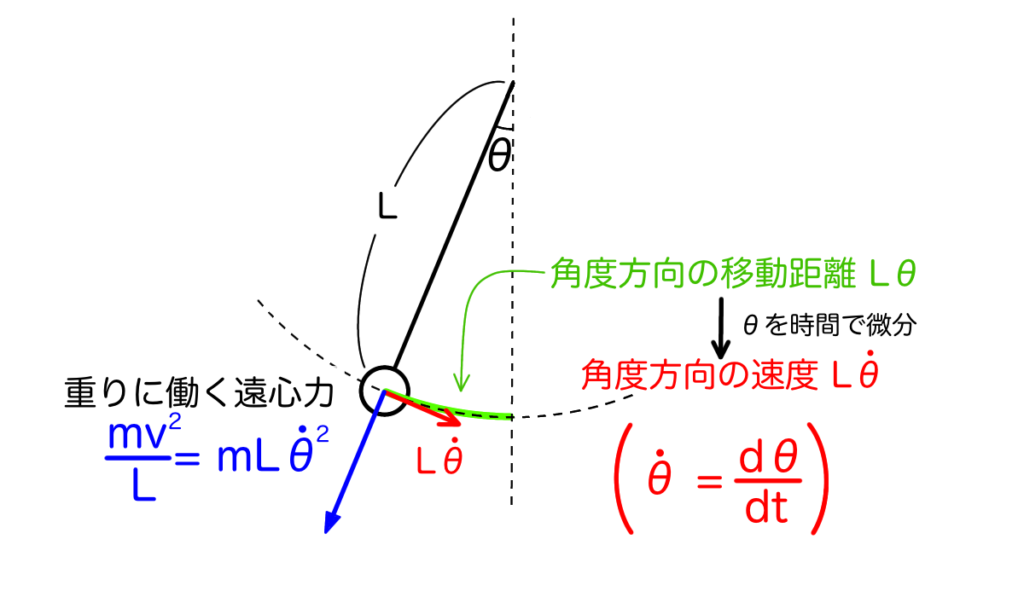
一方、紐の長さを\(L\)、重りの速度を\(v\)とすると重りに働く遠心力は\(\frac{mv^2}{L}\)で表されます。ただし、重りは円運動をしているので角度方向の速度で表した方が便利です。角度\(\theta\)の時間変化、すなわち角速度を\(\dot{\theta}\)と表すと、角度方向の速度は\(L\dot{\theta}\)と表すことができます。これを遠心力の\(v\)に代入すると角度方向の速度を用いて表示した遠心力\(mL\dot{\theta^2}\)が得られます。
以上より、紐の両端に働く張力の大きさは次のように求まります。
$$ T = mg \cos \theta + m L \dot{\theta^2} $$さらに、振り子の振れ幅が小さく\(\theta \ll \frac{\pi}{2} \)が成り立つ領域を考えると\(\cos \theta = 1 -\frac{1}{2}\theta^2\)と近似できます。
$$ T = mg \left( 1 -\frac{1}{2} \theta^2 \right) + m L \dot{\theta^2}\tag{1} $$紐をゆっくり引っ張る時にする仕事を求めるには、張力\(T\)の時間平均\(\langle T \rangle\)が必要です。(1)式の中で時間に依存するのは\(\theta\)だけです。これを求めるために、単振動としての振り子の運動方程式をおさらいしましょう。
振り子の運動方程式
ニュートン力学では物体に働く力\(F\)が物体の質量\(m\)と加速度\(a\)の積に等しいことが知られています。つまり\(F=ma\)という関係が成り立っています。今、考えている振り子は紐が固定されている点を中心に円運動を一部切り取ったような動きをしているので、紐が伸び縮みしない限り円の動径方向には変位が生じません。
従って、極座標系を選ぶと動径方向の運動方程式は消えるから、角度方向の運動方程式一つだけ考えれば良くなります。すなわち解くべき方程式は \(F_\theta=ma_\theta\) ということになります。
すでに求めたように、角度方向の力は\(F_\theta=-mg\sin \theta\)と表すことができます。マイナスがついているのは、角度\(\theta\)の方向とは常に逆方向に力が働いているからです。
また、加速度は速度を時間で微分すればいいので\(a_\theta = L\ddot{\theta}\) と表すことができます。従って、振り子の角度方向の運動方程式は次のようになります。
$$ -mg \sin \theta = m L \ddot{\theta}\tag{2} $$(2)式を整理すると、
$$ \ddot{\theta} = \: -\frac{g}{L} \sin \theta $$さらに、\(\theta\)が十分小さい場合のみを考えることにすると、\(\sin \theta \approx \theta\)と近似できるので、
$$ \ddot{\theta} = \: -\frac{g}{L} \theta $$この微分方程式は簡単に解けます。2階微分するとマイナスがついて元に戻るのは三角関数です。時刻\(t=0\)の時、振り子が最大振幅とっているという初期状態を採用し、係数\(\frac{g}{L}\)が出るように関数を決めると、次のような解が求まります。
$$ \theta = A \cos (2 \pi \nu t) \tag{3} $$ただし
$$ \nu=\frac{1}{2\pi}\sqrt{\frac{g}{L}} \tag{4} $$は振り子の振動数、\(A\)は積分によって出てくる任意の定数で振り子の振幅を表しています。これで振り子の運動方程式とその解を導くことができました。
張力の時間平均と紐をゆっくり引っ張る時の仕事
(3)式を(1)式に代入すると次のようになります。
$$ T = mg-mgA^2 \left\{ \frac{1}{2}\cos^2(2 \pi \nu t)-\sin^2(2 \pi \nu t) \right\} \tag{5} $$この張力に逆らって、ゆっくり紐を引っ張るとき、結果的に手のする仕事は張力の時間平均と引っ張った紐の長さの積に比例するはずです。(5)式において\(\{ \quad \}\)の中は時間的に変動する成分ですので、この部分の時間平均を求めてみましょう。\(\sin\)関数も\(\cos\)関数も\(( \quad )\)の中身の形式によらず、\(0\)から\(2\pi\)までの周期関数ですので、\(\sin \alpha\)、\(\cos \alpha\)とおいて\(0 < \alpha < 2\pi \)の範囲で平均値を求めます。
$$ \frac{1}{2\pi}\int_{0}^{2\pi} \left( \frac{1}{2} \cos^2 \alpha-\sin^2 \alpha \right) d\alpha = -\frac{1}{4} $$これを(5)式に代入すると、
$$ \langle T \rangle = mg + \frac{1}{4}mgA^2 $$となります。ここから紐を引っ張った時にする仕事が求まります。
$$ dW = \: -\langle T \rangle dL = \: -\left( mgdL + \frac{1}{4}mgA^2dL \right) \tag{6} $$(6)式の第1項は重りを全体として上に引き上げるために必要な位置エネルギーを意味していますので、振り子が振れていても止まっていても変わりありません。一方、第2項は振り子の振幅\(A\)が含まれており、振り子が運動していることによって獲得できるエネルギーであることがわかります。つまり振り子を断熱的にゆっくりと引っ張るとによって振り子は
$$ dE = \: -\frac{1}{4}mgA^2dL \tag{7} $$だけの振動のエネルギーを獲得することができるのです。
振り子の断熱不変量
さて、準備が整いましたのえで、いよいよ振り子の断熱不変量を求めましょう。
定常状態で揺れている振り子は位置エネルギーと運動エネルギーを持っています。重りが真下に下がっている時を位置エネルギーの原点としたとき、振り子の持っている全力学的エネルギー\(E\)は次の式で表されます。
$$ E=\frac{1}{2} m L^2 \dot{\theta^2} + \frac{1}{2}mgL\theta^2 \tag{8} $$(8)式の第1項は運動エネルギーを、第2項は位置エネルギーを表しています。なお、ここでも\(\theta\)が小さいと仮定して\(\cos \theta \approx 1 – \frac{1}{2}\theta^2\) という近似式を用いました。(3)式を(8)式に代入して整理すると、
$$ E=\frac{1}{2} m g A^2 L $$となります。この式に時間を含まないことから振り子の全力学的エネルギーが時間によらず一定に保たれることがわかります。
また、(4)式より振動数\(\nu\)を紐の長さ\(L\)で微分すると、
$$ d \nu = -\frac{\nu}{2} \frac{dL}{L} $$が求まります。この式の\(dL\)と\(L\)に、それぞれ(7)式と(8)式を代入して整理すると、
$$ \frac{d\nu}{\nu} = \frac{dE}{E} \tag{9} $$となります。(9)式の両辺を積分すると、
\begin{eqnarray} \int \frac{d\nu}{\nu} &=& \int \frac{dE}{E} \\ \ln{|\nu|} &=& \ln{|E|} + C \\ \ln{\left|\frac{E}{\nu}\right|} &=& -C \\ \end{eqnarray}\(E\)も\(\nu\)も正の値しか取らないので絶対値記号は外すことができます。従って、
$$ \frac{E}{\nu} = e^{-C} \quad (一定) $$という関係が得られます。つまり断熱的にゆっくり振り子の紐を引っ張ると、その仕事の一部は振り子の振動エネルギーとして蓄えられるため、振り子の全力学的エネルギー\(E\)も振動数\(\nu\)も変化しますが、これらの比\(\frac{E}{\nu}\)は一定に保たれるということです。これがまさに断熱不変量です。
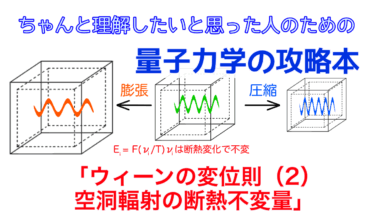
振り子の断熱不変量は同じ単振動である空洞内の電磁波においても同様に成立します。例えば空洞の中に存在するある単一の周波数\(\nu_i\)を持った、エネルギー\(E_i\)の電磁波があったとします。この電磁波の振動周期よりも十分ゆっくり空洞の大きさを変化させると、振動数とエネルギーも次第に変化しますが、断熱不変量\(\frac{E_i}{\nu_i}\)は一定に保たれるのです。
一方で、この断熱不変量はエネルギーと周波数で構成されており温度が入っていません。温度\(T\)を含む断熱不変量を求めるためには、少し複雑な熱力学的考察が必要ですので、その詳細は次の記事に譲ることにします。
まとめ
今回はウィーンの変位則の中で中心的な役割を果たす断熱不変量という概念を、振り子という単振動のモデルを用いて説明しました。
振り子が振動する周期よりも十分遅い周期で振り子の紐をたぐり寄せると、その仕事の一部が振り子の振動エネルギーとして蓄えられます。これによって振り子の振動数も変化しますが、増加したエネルギーと振動数の比は一定に保たれます。
この時、断熱不変量が現れる原因となっているのは振り子を吊るしている紐の張力が、重力や遠心力によって時間的に変動していることにあります。言い方を変えると、振り子が紐を通して外界に対して周期的な力を及ぼしていると考えることができます。
次の記事では、この考え方を空洞内における電磁波に適用し、電磁波が空洞の壁に及ぼす力を考えることで、空洞輻射の断熱不変量が空洞内の温度とどのような関係にあるのかを考察しようと思います。
最後までお読みいただき、どうもありがとうございました。