産業革命が進むイギリスにおいて、製鉄業の発展に伴い高温になった鉄の温度と、そこから発せられる光の色との関係が注目されるようになりました。当時の古典物理学にを用いた考え方では、この温度と光の色の関係を説明することができませんでした。これがいわゆる黒体輻射問題です。そして、この黒体輻射問題に取り組むうちに、人類は量子力学という全く新しい学問分野の扉を開くことになるのです。
黒体輻射問題と時代背景
時は18世紀半ば、イギリスでは石炭を主要エネルギーとした蒸気機関の出現を機に、工場制機械工業の誕生による驚異的な生産力の向上とそれに伴う社会構造の変化が起こります。これがいわゆる産業革命です。この産業革命において最重要産業のひとつだったのは製鉄業です。

産業の急速な工業化を支えたのはいうまでもなく質の高い鉄の大量生産による機械化の推進でした。製鉄工程を効率化するには複雑な鉄鉱石の還元反応を過不足なく進めるための温度管理が大変重要です。しかし、産業革命の時代には1500℃以上の高温になる溶鉱炉の中の温度を正確に測定するのは極めて難しく、職人の技術とカンによって支えられていました。
一方で、物理学の分野においても高温になった物体からはある特定の波長分布をもった光が放出される現象が注目されるようになってきました。このような物体の持つ熱エネルギーが光エネルギーとなって物体の外に放出される現象のことを「輻射」と呼びます。プロセイン王国(現在のロシア、カリーニングラード)出身の物理学者キルヒホフ(1824~1887)はこの輻射のスペクトルが物体の温度のみに依存し、物体の種類や形状、大きさによらないことをつきとめました。

さらにキルヒホフは1869年に物体が光を吸収する能力と放出する能力は互いに等しいことを見いだし、光の完全な吸収体は最も効率の高い放射体でもあるという黒体(Black body)の概念を導入しました。この黒体は完全放射体とも呼ばれ光の波長や入射方向、もしくは偏光等に関係なく入射した全ての光を完全に吸収する理想的な物体です。つまり黒体は、ある温度における熱平衡状態において最大の分光輝度を有しおり、入射した光の反射や透過を考慮する必要がないため、輻射現象を考察する上では大変便利な物理モデルです。
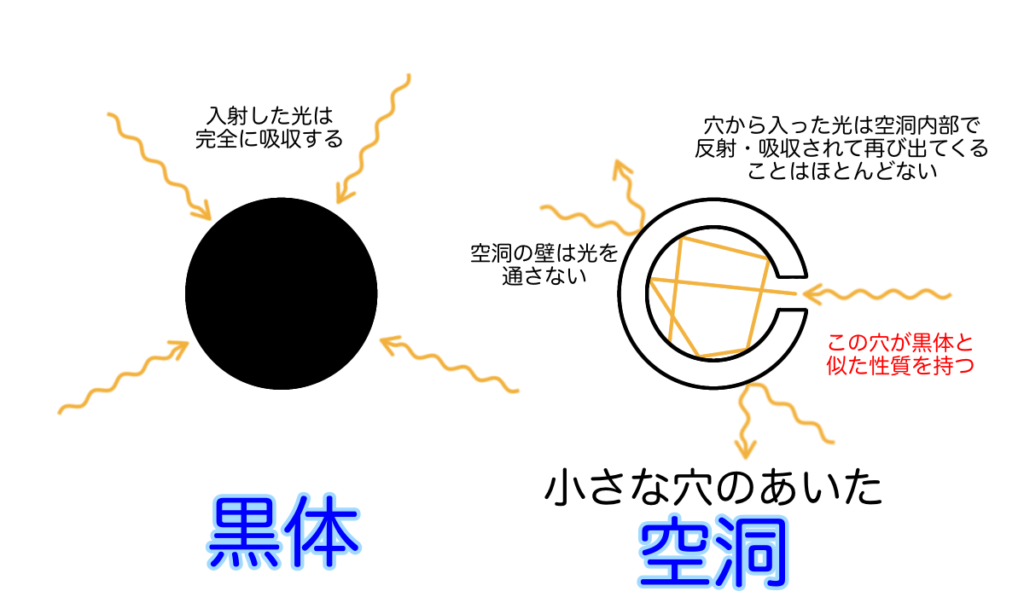
黒体は理想的な物理モデルにすぎませんが、高温に熱せられた溶鉱炉から出てくる光も黒体に極めて類似したスペクトル(波長に対する発光強度の分布)を持つことが明らかになっています。それは黒体と空洞の物理的な性質の類似性を考えると理解できます。空洞内に充満した光エネルギーをわずかに開けた穴から観察する場合、その穴を通って内部に入っていった光はほとんどすべて空洞内部で反射・吸収を繰り返し再び外側に出てくることはありません。従って、小さな穴の空いた空洞という現実に我々が作り出すことのできる実験系が物理モデルである黒体と極めて近い性質を持っていることになります。そのため黒体輻射問題はしばしば空洞輻射問題として扱われることがあります。
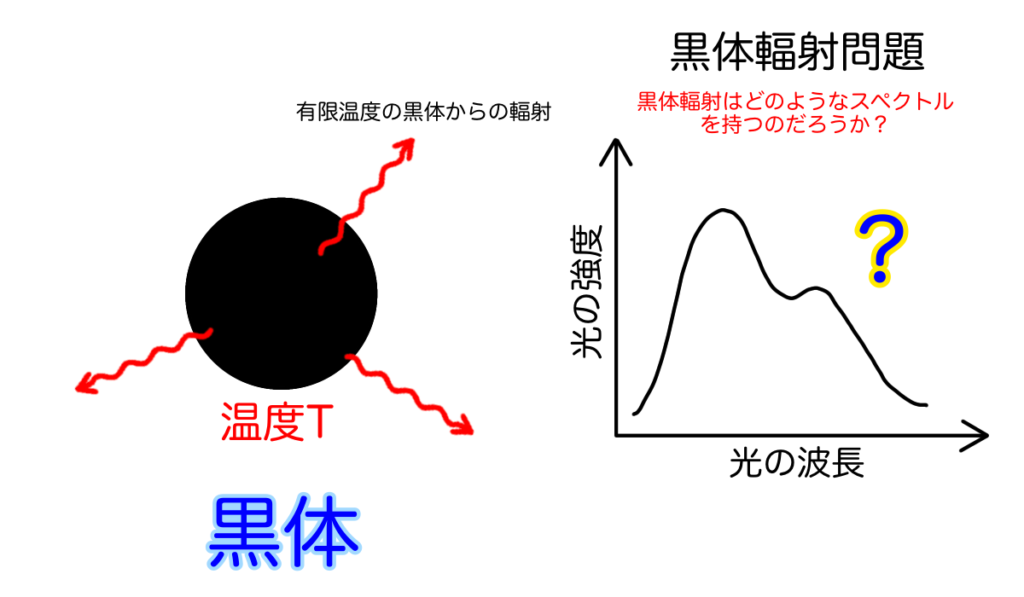
黒体輻射問題とは、一言でいうと「ある温度の黒体から放射される光(黒体輻射)のスペクトルと温度\(T\)の関係を明らかにする」ことです。それまでの研究によって高温物体からの輻射スペクトルはその物体の大きさや形、表面の性質などによらずに物体の温度のみに依存することがわかっていました。つまり、黒体輻射のスペクトルと温度の関係が分かれば、先ほど出てきた溶鉱炉内の温度を、そこから漏れ出る光の波長を測定するだけで知ることができます。ですので当時の物理学者の間でも産業応用上の観点から黒体輻射問題は大変魅力的な研究対象だったに違いありません。
黒体輻射問題が盛んに研究されるようになった19世紀末までには物理学の諸法則は全て完成されていると思われていました。それはニュートン 力学やマクスウェルの電磁気学、そして幾人にもよってまとめ上げられてきた熱力学などです。これらの法則を駆使して当時の物理学者たちは黒体輻射問題に立ち向かいましたが、誰も黒体輻射のスペクトルを説明できませんでした。つまり、黒体輻射問題はこれまで積み上げてきた古典物理学では歯が立たない全く新しい問題であると認識せざるを得なかったのです。
そして、この黒体輻射問題を起点として物理学に大変革が起ります。これこそ量子力学の誕生です。後世を生きる私たちがこの歴史を振り返ると、当時の物理学者たちの挫折や葛藤、そして凄まじいまでの努力と洞察がひしひしと伝わってきます。さて、それではいよいよ量子力学の扉を開きましょう。
空洞内を満たす電磁波のエネルギー密度と輻射強度の関係
ここでは現実に存在し実験で計測可能な空洞輻射の性質について考えていきます。具体的には空洞内部を満たす電磁波のエネルギーと空洞にあいた小さな穴から漏れ出る電磁波のエネルギー流束の関係式を求めます。
初め、何もなかった空洞は温度\(T\)の壁からの輻射によってエネルギーを獲得し、次第に電磁波としてエネルギーを蓄積していきます。やがて空洞内が熱平衡状態に達すると壁の温度\(T\)と同じエネルギーの電磁波で空洞内が満たされます。
壁が光を全く通さない場合、空洞内では全ての場所で同じ密度の当方的な電磁波が存在しており、この状況は熱力学第二法則から空洞の形状や壁の材質によらないことがわかります。もし、電磁波の密度が空洞の形状や材質、あるいは空洞内の場所で異なっている場合、それは熱的平衡状態ではなくエントロピーをさらに増大させる余地があることになるからです。
本来はこの空洞輻射問題は温度\(T\)の物体が放出する電磁波の波長に対する強度分布を理論的に予言することが最終目的ですが、まずは簡単のために電磁波のうち、特定の波長を持ったものだけを考えることにします。
今、空洞内における波長\(\lambda\)の電磁波のエネルギー密度を\(\rho[\mathrm{J/m^3}]\)とします。このエネルギー密度\(\rho\)は温度\(T\)と波長\(\lambda\)のみの関数になります。
空洞輻射のモデルに基づき、空洞内にエネルギー密度\(\rho\)で満たされた電磁波が空洞に開けた小さな穴からどのくらい漏れ出てくるかを考えることにしましょう。穴から漏れ出てくる電磁波はエネルギー流束\(J[\mathrm{J/s \cdot m^2}]\)、すなわち単位時間、単位面積あたりのエネルギーとして測定することができます。
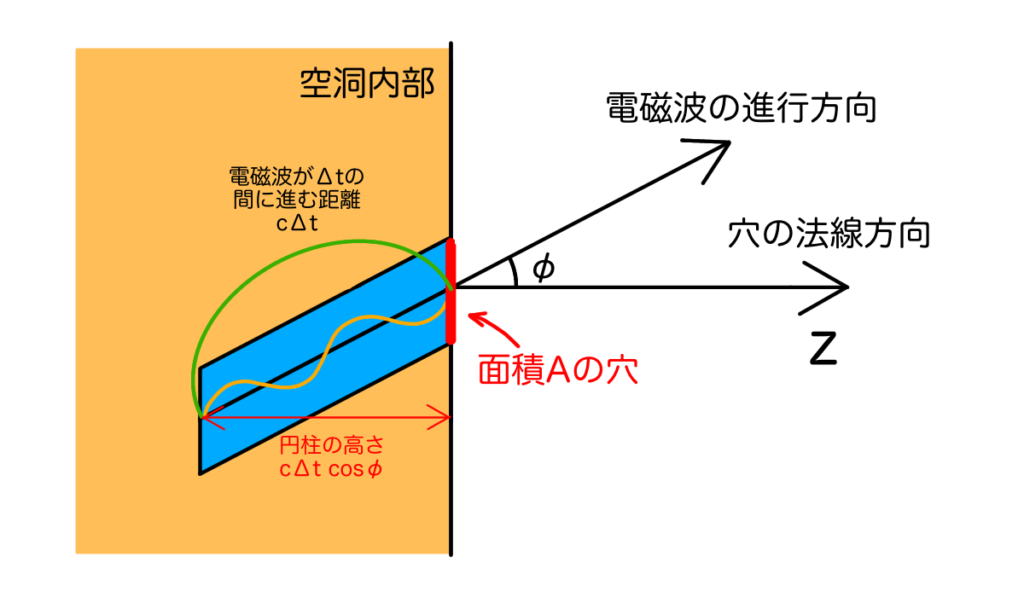
まず、状況を図で整理しましょう。空洞に面積\(A[\mathrm{m^2}]\)の穴が開けられているとします。この穴の法線方向を\(z\)軸とし、穴から出る電磁波の進行方向と\(z\)軸の成す角を\(\phi\)とします。穴を通って時間\(\Delta t\)の間に外に出ることのできる電磁波は、体積\(V = A c \Delta t \cos \phi\)の円筒の中に存在している電磁波です。この体積に空洞内のエネルギー密度をかければ、時間\(\Delta t\)の間に、面積\(A\)の穴から\(\phi\)の方向に出ていくエネルギーがわかります。
ここで気をつける必要があるのはエネルギー密度\(\rho\)には等方的な全ての方向に進む電磁波が含まれていることです。今、注目しているのは穴から出ることのできる\(\phi\)方向に進む電磁波だけです。\(\phi\)方向に進む電磁波が全電磁波のうちどれくらいを占めるかを計算するために、微小立体角\(d \Omega\)を貫く電磁波として捉え直してみます。空洞内の全電磁波のうち立体角\(d \Omega\)を貫く電磁波の割合は\(d \Omega / \Omega\)で表すことができます。\(\Omega\)は球全体の立体角であり\(4\pi\)という定数ですので、\(d \Omega\)を貫く電磁波のエネルギー密度は\(\rho d \Omega / 4 \pi\)となります。
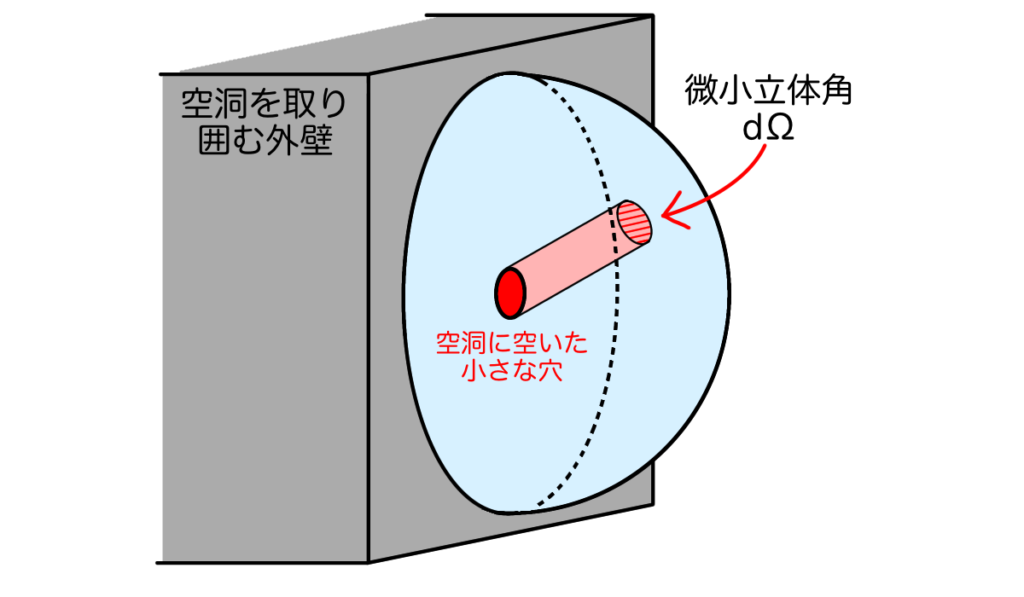
以上より空洞に開けた面積\(A\)の穴から立体角\(d \Omega\)の方向に漏れ出てくる電磁波のエネルギーは
$$ \frac{\rho A c \Delta t \cos \phi}{4 \pi}d \Omega $$と表されます。これをエネルギー流束に直すために、穴の面積\(A\)と時間\(\Delta t\)で割ると、微小立体角\(d \Omega\)に対応する微小エネルギー流束流束\(d J\)が求まります。
$$ dJ[\mathrm{J/s \cdot m^2}] = \frac{\rho c \cos \phi}{4 \pi}d \Omega $$さて、ここから空洞輻射全体のエネルギー流束を求めるには半球面上にわたって\(d\Omega\)で上式を積分すればOKです。
$$ J[\mathrm{J/s \cdot m^2}] = \int_{半球面} \frac{\rho c \cos \phi}{4 \pi}d \Omega $$上式の被積分関数は今天頂角\(\phi\)のみの関数であり、方位角\(\theta\)には依存していません。従って、微小立体角\(d\Omega\)は次の図から明らかなように微小天頂角\(\phi\)の関数として書き直すことができます。
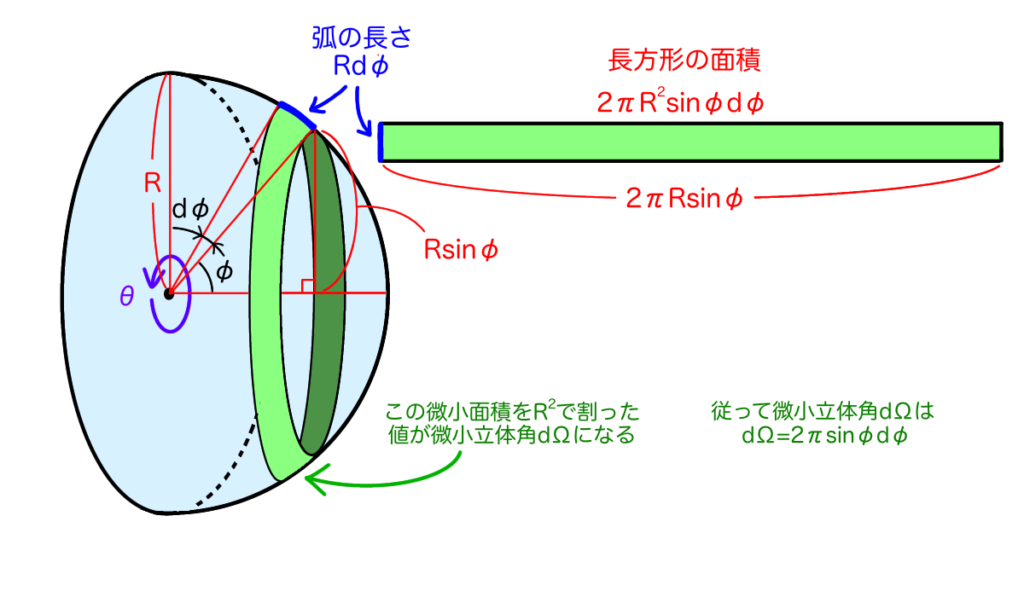
上図を見れば明らかなように、半球面上における立体角\(d\Omega\)の積分を実行するとき、天頂角\(d\phi\)は\(0\)から\(\frac{\pi}{2}\)まで動きます。
以上より\(d\Omega\)に対する半球面上の積分は\(d\phi\)に対する\(0 \sim \frac{\pi}{2}\)の積分に直すことができて、これを実行すると空洞輻射のエネルギー流束が求まります。
$$ \begin{eqnarray} J[\mathrm{J/s \cdot m^2}] &=& \int_{0}^{\frac{\pi}{2}} \frac{1}{2} \rho c \cos \phi \sin \phi d \phi \\ &=& \frac{\rho c}{4} \int_{0}^{\frac{\pi}{2}} \sin 2\phi d \phi \\ &=& \frac{c \rho}{4} \end{eqnarray} $$さらに、空洞輻射の表面輝度を単位立体角あたりのエネルギー流束と定義すれば、表面輝度\(J_0\)は\(J\)を半球分の立体角\(2\pi\)で割ればいいので、
$$ J_0[\mathrm{J/s \cdot m^2 \cdot sr}] = \frac{c \rho}{8\pi} $$となります。以上の議論により光を通さない壁で囲まれた空洞内部の電磁波のエネルギー密度と空洞輻射の表面輝度の関係が明らかになりました。この関係式から\(J\)、もしくは\(J_0\)は\(\rho\)の定数倍になっているため空洞輻射の表面輝度は空洞内部のエネルギー密度と同じスペクトル(波長依存性)を持つことがわかります。すなわち実験的に空洞輻射の輝度の波長分解計測を行えば、そこから空洞内部のエネルギー密度のスペクトルを知ることができるということです。
また、光を全く通さない壁で囲まれた空洞に開いた面積\(A\)からの出てくる輻射は、同様の壁に埋め込まれた表面積\(A\)の黒体からの輻射と同じ性質を持つことも付け加えて置きます。
以上の議論から、空洞内のエネルギー密度\(\rho\)の波長依存性を理論的に求めることができれば、実験結果と直接比較可能なモデルを作ることができることがわかりました。冒頭でも触れたように、このエネルギー密度を導く過程で古典力学の限界が顕になり、量子力学への扉が開かれることになります。